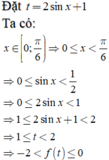Cho x,y là các số thực thuộc (0;1) thỏa mãn (x3+y3)(x+y)xy =(1−x)(1−y).Tìm giá trị lớn nhất của biểu thức P=1√1+x2 +1√1+y2 +4xy−x2−y2

Những câu hỏi liên quan
Cho các số thực x,y,z thuộc [-1,2] thỏa mãn x+y+z=0.Chứng minh
a,\(x^2\)+\(y^2\)+\(z^2\)\(\le\)6
b,\(x^2\)+\(y^2\)+\(z^2\)\(\le\)2xyz+2
Do \(x\in\left[-1;2\right]\Rightarrow\)\(\left(x+1\right)\left(x-2\right)\le0\Leftrightarrow x^2\le x+2\)
Tương tự: \(y^2\le y+2\) ; \(z^2\le z+2\)
Cộng vế: \(x^2+y^2+z^2\le x+y+z+6=6\) (đpcm)
Mặt khác \(x;y;z\in\left[-1;2\right]\Rightarrow\left(x+1\right)\left(y+1\right)\left(z+1\right)\ge0\)
\(\Leftrightarrow xyz+xy+yz+zx+x+y+z+1\ge0\)
\(\Leftrightarrow xyz+xy+yz+zx+1\ge0\)
\(\Leftrightarrow2xyz+2\ge-2\left(xy+yz+zx\right)\)
\(\Leftrightarrow2xyz+2\ge\left(x^2+y^2+z^2\right)-\left(x+y+z\right)^2\)
\(\Leftrightarrow2xyz+2\ge x^2+y^2+z^2\) (đpcm)
Đúng 1
Bình luận (0)
Cho hàm số y f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) m có nghiệm thuộc khoảng
0
;
π
là
Đọc tiếp
Cho hàm số y = f(x) liên tục trên R và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sin x) = m có nghiệm thuộc khoảng 0 ; π là

![]()
![]()
![]()
![]()
Cho a;b;c là các số thực khác 0 thuộc R
tìm x; y;; z khác 0 sao cho
\(\frac{xy}{ay+bx}=\frac{yz}{bz+cy}=\frac{zx}{cx+az}\frac{x^2+y^2+z^2}{a^2+b^2+c^2}\)
\(\frac{xy}{ay+bx}=\frac{yz}{bz+cy}=\frac{zx}{cx+az}=\frac{x^2+y^2+z^2}{a^2+b^2+c^2}\)
\(\Leftrightarrow\frac{x}{a}+\frac{y}{b}=\frac{y}{b}+\frac{z}{c}=\frac{z}{c}+\frac{x}{a}\)
\(\hept{\begin{cases}\frac{x}{a}+\frac{y}{b}=\frac{y}{b}+\frac{z}{c}\Rightarrow\frac{x}{a}=\frac{z}{c}\\\frac{z}{c}+\frac{x}{a}=\frac{y}{b}+\frac{z}{c}\Rightarrow\frac{x}{a}=\frac{y}{b}\\\frac{x}{a}+\frac{y}{b}=\frac{z}{c}+\frac{x}{a}\Rightarrow\frac{y}{b}=\frac{z}{c}\end{cases}}\Rightarrow\frac{x}{a}=\frac{z}{c}=\frac{y}{b}.\text{đăt}k=\frac{x}{a}=\frac{z}{c}=\frac{y}{b}\Rightarrow x=ak,z=ck,y=bk\)
ta có: \(\frac{x^2+y^2+z^2}{a^2+b^2+c^2}=\frac{k^2.\left(x^2+y^2+z^2\right)}{\left(x^2+y^2+z^2\right)}=k^2\Rightarrow k^2=2k\Rightarrow k^2-2k=0\Rightarrow k.\left(k-2\right)=0\)
\(\Rightarrow\orbr{\begin{cases}k=0\\k=2\end{cases}\text{mà a,b,c và x,y,z khác 0. }\Rightarrow k=2\Rightarrow x=2a,y=2b,z=2c}\)
p/s: bài nì khó chơi vc =.=" sai sót bỏ qua ^^'
Đúng 1
Bình luận (0)
tại sao k^2 lại bằng 2k
Vì x, y, z khác 0
=> xy khác 0 ; yz khác 0 ; zx khác 0
Theo bài ra ta thấy : đổi chỗ của tử số và mẫu số thì đẳng thức vẫn xảy ra nên ta có:
ay+bx/xy=bz+cy/yz=cx+az/zx=a^2+b^2+c^2/x^2+y^2+z^2 (3)
=>a/x + b/y = b/y + c/z = c/z + a/x
=> a/x = b/y =c/z
Đặt a/x = b/y = c/z = k ta suy ra
x=ak; y=bk, z=ck
Ta có :
ay+bx/xy = a.bk+b.ak/ak.bk = 2.abk/abk.k = 2/k (1)
Lại có : a^2+b^2+c^2/x^2+y^2+z^2
= a^2+b^2+c^2/k^2 ( a^2 +b^2 +c^2 )
=1/k^2 (2)
(1)(2)(3) => 2/k = 1/k^2
=>k^2/k=1/2
=>k=1/2
Với k=1/2 =>x= 1/2 .a ; y = 1/2 b ; z= 1/2 .c
Vậy với mọi x, y, z thỏa mãn điều kiện trên thì mọi kết quả đều đúng.
Hãy bày tỏ cảm xúc và bài làm của mình nha.Trân thành cảm ơn.
Cho hàm số yf(x) liên tục trên
ℝ
và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sin x +1) m có nghiệm thuộc nửa khoảng
[
0
;
π
6
)
là: A. (-2;0] B. (0;2] C. [-2;2) D. (-2;0)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên ℝ và có đồ thị như hình vẽ. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(2sin x +1) = m có nghiệm thuộc nửa khoảng [ 0 ; π 6 ) là:
A. (-2;0]
B. (0;2]
C. [-2;2)
D. (-2;0)
cho a,b,c là các số thực # 0. Tìm các số thực x,y,z #0 thỏa mãn: x*y/a*y+b*x=y*z/b*z+c*y=z*x/c*x+a*z=(x^2+y^2+z^2)/(a^2+b^2+c^2)
Cho a,b,c là các số thực # 0. Tìm x,y,z là số thực # 0 thỏa mãn x*y/a*y+b*x=y*z/b*z+c*y=z*x/c*x+a*z=(x^2+y^2+z^2)/(a^2+b^2+c^2)
Cho x,y,z là các số thực thuộc đoạn [0:4]. Tìm giá trị lớn nhất của :P= \(\sqrt{xy}\left(x-y\right)+\sqrt{yz}\left(y-z\right)+\sqrt{zx}\left(z-x\right)\)
Cho hàm số y f (x) liên tục trên
ℝ
và có đồ thị như hình vẽ bên.Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) m có nghiệm thuộc khoảng (0;
π
) là A. [-1;3) B. (-1;1) C. (-1;3) D. [-1;1 )
Đọc tiếp
Cho hàm số y = f (x) liên tục trên ℝ và có đồ thị như hình vẽ bên.
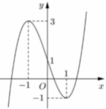
Tập hợp tất cả các giá trị thực của tham số m để phương trình f (sinx) = m có nghiệm thuộc khoảng (0; π ) là
A. [-1;3)
B. (-1;1)
C. (-1;3)
D. [-1;1 )
Cho hàm số yf(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)m có nghiệm thuộc khoảng
0
;
π
là A. (-1;3) B. (-1;1) C. (-1;3) D. (-1;1)
Đọc tiếp
Cho hàm số y=f(x) liên tục trên R và có đồ thị như hình vẽ bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f(sinx)=m có nghiệm thuộc khoảng 0 ; π là
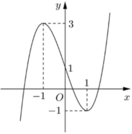
A. (-1;3)
B. (-1;1)
C. (-1;3)
D. (-1;1)
Cho hàm số y f(x) liên tục trên
ℝ
và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình
f
(
e
x
)
m
có nghiệm thuộc khoảng (0; ln 3) là: A. (1;3) B.
-
1
3
;
0
C....
Đọc tiếp
Cho hàm số y = f(x) liên tục trên ℝ và có đồ thị như hình bên. Tập hợp tất cả các giá trị thực của tham số m để phương trình f ( e x ) = m có nghiệm thuộc khoảng (0; ln 3) là:
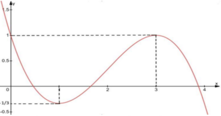
A. (1;3)
B. - 1 3 ; 0
C. - 1 3 ; 1
D. - 1 3 ; 1