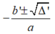Cho tam thức bậc hai f(x)=ax2+bx+c,a>0,a,b,c\(\in\)Z
tm f(x) có 2 nghiệm phân biệt trong khoảng(0;1) CMR a>/=5
Những câu hỏi liên quan
Cho tam thức bậc hai
f
(
x
)
a
x
2
+
b
x
+
c
có hai nghiệm thực phân biệt
x
1
,
x
2
Tính tích phân
∫
x
1
x
2
(...
Đọc tiếp
Cho tam thức bậc hai f ( x ) = a x 2 + b x + c có hai nghiệm thực phân biệt x 1 , x 2 Tính tích phân ∫ x 1 x 2 ( 2 a x + b ) 3 . e a x 2 + b x + c d x
Cho tam thức bậc hai
f
x
a
x
2
+
b
x
+
c
,
a
,
b
,
c
∈
ℝ
,
a
≠
0
có hai nghiệm thực phân biệt
x
1
,...
Đọc tiếp
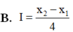
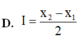
Cho tam thức bậc hai f x = a x 2 + b x + c , a , b , c ∈ ℝ , a ≠ 0 có hai nghiệm thực phân biệt x 1 , x 2 . Tính tích phân I = ∫ x 1 x 2 2 a x + b 3 . e a x 2 + b x + c d x
A. I = x 2 − x 1
B. I = x 2 − x 1 4
C. I = 0
D. I = x 2 − x 1 2
Cho đa thức bậc hai F(x) = ax2 + bx + c, trong đó, a,b và c là những số với a \( \ne \) 0
a) Cho biết a + b + c = 0. Giải thích tại sao x = 1 là một nghiệm của F(x)
b) Áp dụng, hãy tìm một nghiệm của đa thức bậc hai 2x2 – 5x + 3
a) Thay x = 1 vào đa thức F(x), ta có:
F(1) = a.12 + b.1 + c = a+ b + c
Mà a + b + c = 0
Do đó, F(1) = 0. Như vậy x = 1 là một nghiệm của F(x)
b) Ta có: Đa thức 2x2 – 5x + 3 có a = 2 ; b = -5; c = 3 nên a + b + c = 2 + (-5) + 3 = 0
Do đó, đa thức có 1 nghiệm là x = 1
Đúng 1
Bình luận (0)
Cho hàm số
f
(
x
)
x
3
+
a
x
2
+
b
x
+
c
. Nếu phương trình
f
(
x
)
0
có ba nghiệm phân biệt thì phương trình
2
f
(
x
)
.
f
”
(
x
)...
Đọc tiếp
Cho hàm số f ( x ) = x 3 + a x 2 + b x + c . Nếu phương trình f ( x ) = 0 có ba nghiệm phân biệt thì phương trình 2 f ( x ) . f ” ( x ) = [ f ’ ( x ) ] 2 có nhiều nhất bao nhiêu nghiệm?
A. 1 nghiệm
B. 4 nghiệm
C. 3 nghiệm
D. 2 nghiệm
Cho đa th ức f(x )= ax
2
+bx+c có a+b+c=0 ho ặc a -b+c=0. Chứng minh
r ằng đa thức f(x) có ít nhất một nghiệm
\(f\left(x\right)=ax^2+bx+c\)
Ta có: \(f\left(1\right)=a+b+c;f\left(-1\right)=a-b+c\)
Khi \(a+b+c=0\Rightarrow f\left(1\right)=0\Rightarrow x=1\) là nghiệm đa thức
Khi \(a-b+c=0\Rightarrow f\left(-1\right)=0\Rightarrow x=-1\) là nghiệm đa thức
Vậy đa thức có ít nhất 1 nghiệm.
Đúng 1
Bình luận (0)
Cho tam thức bậc hai f(x) = a x 2 + bx + c, (a ≠ 0) có biệt thức Δ = b 2 - 4ac. Chọn khẳng định đúng:
A. Nếu Δ < 0 thì af(x) > 0, ∀x ∈ R
B. Nếu Δ > 0 thì af(x) < 0, ∀x ∈ R
C. Nếu Δ ≤ 0 thì af(x) ≥ 0, ∀x ∈ R
D. Nếu Δ ≥ 0 thì af(x) > 0, ∀x ∈ R
Đáp án A.
Ta có: nếu Δ < 0 thì f(x) luôn cùng dấu với hệ số a với mọi giá trị của x, tức là af(x) > 0, ∀x ∈ R
Đúng 0
Bình luận (0)
Xét hai câu sau:
P: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt”;
Q: “Phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\)”.
a) Hãy phát biểu mệnh đề \(P \Rightarrow Q\).
b) Hãy phát biểu mệnh đề \(Q \Rightarrow P\).
Mệnh đề \(P \Rightarrow Q\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\).”
Mệnh đề \(Q \Rightarrow P\): “Nếu phương trình bậc hai \(a{x^2} + bx + c = 0\) có biệt thức \(\Delta = {b^2} - 4ac\;\, > 0\) thì phương trình bậc hai \(a{x^2} + bx + c = 0\) có hai nghiệm phân biệt.”
Đúng 0
Bình luận (0)
Cho phương trình: f(x)=ax2+bx+c=0 trong đó a,b,c thuộc Z và a>0 có 2 nghiệm phân biệt trong khoảng (0,1). tìm GTNN của a
phương trình delta
Cho phương trình
a
x
2
+
b
x
+
c
0
(
a
≠
0
)
có biệt thức b 2b;
Δ
b
2
-
a
c
. Phương trình đã cho có hai nghiệm phân biệt khi: A.
△
0 B.
△
0 C.
△
≥
0...
Đọc tiếp
Cho phương trình a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c . Phương trình đã cho có hai nghiệm phân biệt khi:
A. △ ' > 0
B. △ ' = 0
C. △ ' ≥ 0
D. △ ' ≤ 0
Đáp án A
Xét phương trình bậc hai a x 2 + b x + c = 0 ( a ≠ 0 ) có biệt thức b = 2b'; Δ ' = b ' 2 - a c :
• TH1: Nếu Δ' < 0 thì phương trình vô nghiệm
• TH2: Nếu Δ' = 0 thì phương trình có nghiệm kép
x
1
=
x
2
= 
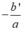
• TH3: Nếu Δ' > 0 thì phương trình có hai nghiệm phân biệt
x
1
,
2
= 
Đúng 0
Bình luận (0)