Các câu hỏi tương tự
Cho tam thức bậc hai f(x) = a x 2 + bx + c, (a ≠ 0) có biệt thức Δ = b 2 - 4ac. Chọn khẳng định đúng:
A. Nếu Δ < 0 thì af(x) > 0, ∀x ∈ R
B. Nếu Δ > 0 thì af(x) < 0, ∀x ∈ R
C. Nếu Δ ≤ 0 thì af(x) ≥ 0, ∀x ∈ R
D. Nếu Δ ≥ 0 thì af(x) > 0, ∀x ∈ R
Đồ thị hàm số
y
f
(
x
)
a
x
2
+
b
x
+
c
được cho trong hình 47. Kí hiệu
Δ
b
2
-
4
a
c
là biệt số của f(x). Trong các khẳng định sau, kh...
Đọc tiếp
Đồ thị hàm số y = f ( x ) = a x 2 + b x + c được cho trong hình 47. Kí hiệu Δ = b 2 - 4 a c là biệt số của f(x). Trong các khẳng định sau, khẳng định nào sai?
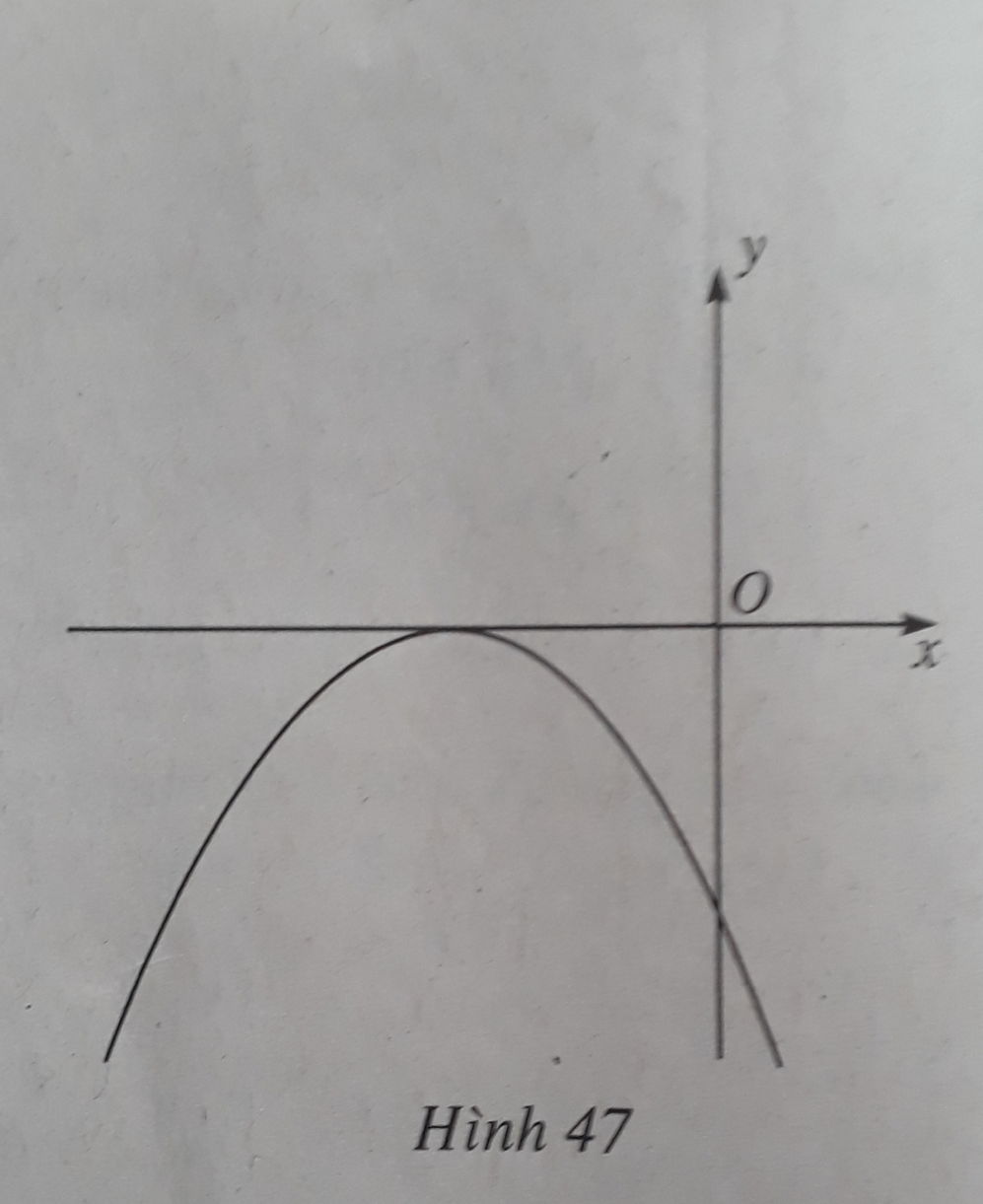
A. a, b trái dấu
B. f(x) ≤ 0, ∀x
C. a < 0, c < 0
D. Δ = 0, a < 0
cho f(x) = ax2 + bx + c ( a≠0). Điều kiện để f(x) > 0, ∀x∈R
Cho f(x)=x^2 -2(m-2)x+m+10. Định m để:
a. Phương trình f(x)=0 có một nghiệm x= 1 và tính nghiệm kia
b. Phương trình f(x)=0 có nghiệm kép. Tính nghiệm kép đó.
c. Tìm m để phương trình f(x)=0 có 2 nghiệm âm phân biệt.
d. Tìm m để f(x)<0 có nghiệm đúng với mọi xϵR
Cho parabol (P): y a
x
2
+ bx + c (a
≠
0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| m có bốn nghiệm phân biệt. A. −1 m 3 B. 0 m 3. C. 0
≤
m
≤
3. D. −1
≤
m
≤
3.
Đọc tiếp
Cho parabol (P): y = a x 2 + bx + c (a ≠ 0) có đồ thị như hình bên. Tìm các giá trị m để phương trình |ax2 + bx + c| = m có bốn nghiệm phân biệt.
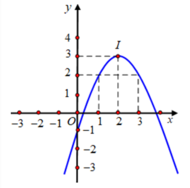
A. −1 < m < 3
B. 0 < m < 3.
C. 0 ≤ m ≤ 3.
D. −1 ≤ m ≤ 3.
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau: Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu. Bước 2: Với điều kiện a, c trái dấu ta có a.c 0 suy ra Δ b2 - 4ac 0. Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm. Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu. Lập luận trên sai từ bước nào? A. Bước 1 B. Bước 2 C. Bước 3 D. Bước 4.
Đọc tiếp
Chứng minh rằng: “Nếu phương trình bậc hai : ax2 + bx + c = 0 vô nghiệm thì a và c cùng dấu”. Một học sinh đã làm như sau:
Bước 1: Giả sử phương trình vô nghiệm và a, c cùng dấu.
Bước 2: Với điều kiện a, c trái dấu ta có a.c > 0 suy ra Δ = b2 - 4ac > 0.
Bước 3: Nên phương trình có hai nghiệm phân biệt, điều này mâu thuẫn với giả thiết phương trình vô nghiệm.
Bước 4: Vậy phương trình vô nghiệm thì a, c phải cùng dấu.
Lập luận trên sai từ bước nào?
A. Bước 1
B. Bước 2
C. Bước 3
D. Bước 4.
Cho đa thức f(x) = a x 2 + bx + c. Xét mệnh đề "Nếu a + b + c = 0 thì f(x) có một nghiệm bằng 1". Hãy phát biểu mệnh đề đảo của mệnh đề đảo của mệnh đề trên. Nêu một điều kiện cần và đủ f(x) có một nghiệm bằng 1
Giải bất phương trình bậc hai :
Loại 1) Khi phương trình bậc hai có 2 nghiệm phân biệt:
a) 2x^2+x-3>0
b x^2+3x-1>0 c) 4x^2-1<'or'=0 d)x^2+5x+6>'or'=0
e) x^2+3x+2<'or'=0 f)x^2+4x+3<0
Cho hàm số f(x) a
x
2
+ bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 m có đúng 2 nghiệm phân biệt. A.
m
≥
0
m
−
1
B. ...
Đọc tiếp
Cho hàm số f(x) = a x 2 + bx + c đồ thị như hình bên dưới. Hỏi với những giá trị nào của tham số m thì phương trình |f(x)| − 1 = m có đúng 2 nghiệm phân biệt.
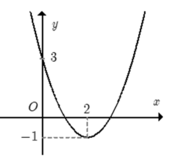
A. m ≥ 0 m = − 1
B. m > 0 m = − 1
C. m ≥ -1
D. m ≥ 0







