Câu 1: (1x3 điểm) Cho hai điểm A (1;-1) B(3;0)
a. Tìm M thuộc trục Ox sao cho tam giác MAB vuông tại M
b. Tìm N thuộc trục Oy sao cho NA=\(\sqrt{2}\).NB
c. Tìm P sao cho ABP vuông tại A và AP=2AB
Chp hàm số f x = 2 x + 3 k h i ≥ 1 x 3 + 2 x 2 - 7 x + 4 x - 1 k h i x < 1 . Tính đạo hàm của hàm số đã cho tại điểm x 0 = 1 ?
A. 0
B. 4
C. 5
D. Đáp án khác
Ta có:
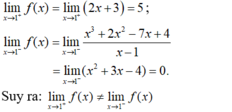
⇒ hàm số không liên tục tại x = 1 nên hàm số không có đạo hàm tại x0 = 1.
Chọn D.
Câu 1. 1. Cho hàm số y=f(x)=1/3x^2 a) Cho hai điểm A và B thuộc đồ thị hàm số có hoành độ lần lượt là –3 và 9 tìm. Tọa độ 2 điểm A và B Vt phương trình đường thẳng đi qua hai điểm A và B
Câu 1
Đoạn thẳng AB là hình gồm
A/ Hai điểm A và B
B/ Tất cả các điểm nằm giữa A và B
C/ Tất cả các điểm nằm giữa A và B và cả A,B
Câu2
Có 1 và chỉ 1 đường thẳng đi qua
a) hai điểm cho trước
b) điểm A cho trước
c) hai điểm phân biệt cho trước
Câu 1: (3 điểm)
Trên bẩn đồ tỉ lệ 1: 2000, khoảng cách giữa hai địa điểm A và B trên bản đồ là 5cm. Hãy tính khoảng cách hai điểm đó ngoài thực tế?
Câu 2: (7 điểm)
a/ Tỉ lệ bản đồ cho ta biết điều gì?
b/ Kí hiệu ở hình bên dưới thuộc loại kí hiệu nào?
Cảng biển
chỉ em với ạ!!
Câu 1: Khoảng cách 2 điểm đó ngoài thực tế : \(2000.5=10000\left(cm\right)=1\left(km\right)\)
Câu 2: Tỉ lệ bản đồ cho biết các khoảng cách trên bản đồ đã được thu nhỏ bao nhiêu lần so với khoảng cách thực của chúng trên thực địa.
Cho bốn điểm A,B,C,D cùng thuộc đường thẳng xy như hình 8.21. Trong các câu sau đây, câu nào đúng ?
1. Điểm B nằm giữa hai điểm A và điểm D
2. Điểm A và điểm C nằm cùng phía đối với điểm D
3. Điểm B nằm khác phía điểm A đối với điểm D
4. Điểm B và điểm C nằm cùng phía đối với điểm D.
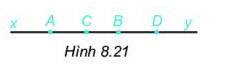
1. Đúng (điểm B nằm giữa A và D).

2. Đúng (A và điểm C nằm cùng phía đối với điểm D)

3. Sai vì điểm B nằm cùng phía điểm A đối với điểm D.
4. Đúng
câu 1: Cho trước 4 điểm A, B, C, D trong đó không có 3 điểm nào thẳng hàng. Tìm điểm O sao cho 3 điểm A, O, C thẳng hàng và 3 điểm B, O, D thẳng hàng.
câu 2 :Cho 2 tia AM, AN đối nhau. Lấy điểm B sao cho điểm N nằm giữa hai điểm A, B. Hỏi A có nằm giữa hai điểm M, N không?
giúp mk với mk còn 10 phút nữa thui
Câu 3: Trong mặt phẳng Oxy, cho hai điểm A(1;-2), B(3;1). Viết phương trình tham số của đường thẳng d đi qua hai điểm A và B.
Câu 4: Cho hai điểm A(4; -3), B(2;1). Viết phương trình đường tròn (C) nhận AB làm đường kính
Câu 4:
Tọa độtâm I là;
x=(4+2)/2=3 và y=(-3+1)/2=-1
I(3;-1); A(4;-3)
IA=căn (4-3)^2+(-3+1)^2=căn 5
=>(C): (x-3)^2+(y+1)^2=5
Câu 3:
vecto AB=(2;3)
PTTS là:
x=1+2t và y=-2+3t
Câu 1 : Trên tia Ox cho hai điểm A và B. Biết OB = 12 cm và OA = 6cm.
a) Điểm A có phải là trung điểm của đoạn thẳng OB không? Vì sao?
b) Gọi I là trung điểm của đoạn thẳng AB. Tính độ dài đoạn thẳng OI.
c) M là điểm thuộc tia đối của tia OB. Biết khoảng cách giữa hai điểm M và I là 12cm. Tính khoảng cách giữa hai điểm O và M.
Câu 2: Tính tổng
A = 100 - 99 + 98 - 97 + ......... + 2 - 1.
Cho hai hàm số y = 4x + 2 (1)và hàm số y = 2x - 2(2)câu a vẽ đồ thị câu b tìm tọa độ giao điểm m của hai hàm số trên câu c tìm tọa độ a b là giao điểm của hai đồ thị hàm số 1 2 với trục ox câu d tính chu vi diện tích tam giác MAB + e tính các góc của tam giác MAB
a:
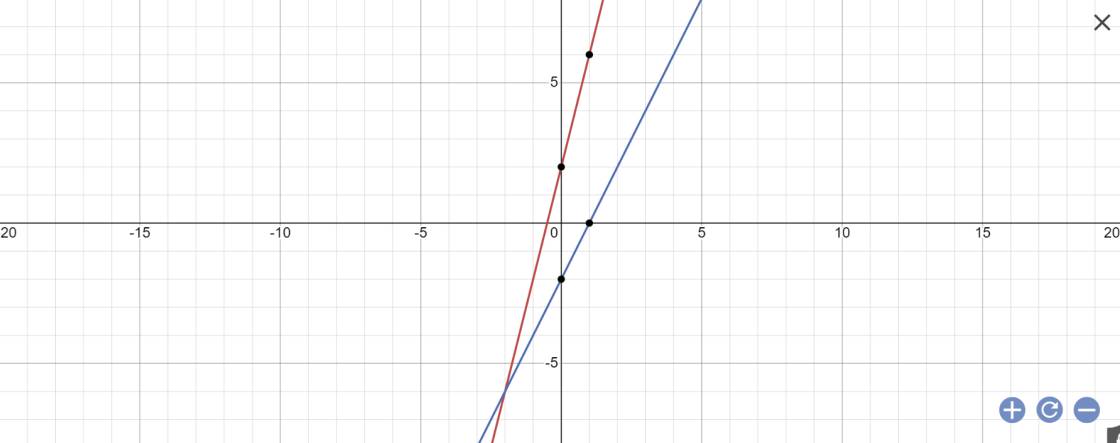
b: phương trình hoành độ giao điểm là:
4x+2=2x-2
=>4x-2x=-2-2
=>2x=-4
=>x=-2
Thay x=-2 vào y=4x+2, ta được:
\(y=4\cdot\left(-2\right)+2=-8+2=-6\)
Vậy: M(-2;-6)
c: Tọa độ A là:
\(\left\{{}\begin{matrix}y=0\\4x+2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\4x=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)
Tọa độ B là:
\(\left\{{}\begin{matrix}y=0\\2x-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\2x=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=0\\x=1\end{matrix}\right.\)
Vậy: B(1;0); A(-1/2;0)
d: M(-2;-6); B(1;0); A(-1/2;0)
\(MA=\sqrt{\left(-\dfrac{1}{2}+2\right)^2+\left(0-6\right)^2}=\dfrac{3\sqrt{17}}{2}\)
\(MB=\sqrt{\left(1+2\right)^2+\left(0+6\right)^2}=3\sqrt{5}\)
\(AB=\sqrt{\left(-\dfrac{1}{2}-1\right)^2+\left(0-0\right)^2}=\dfrac{3}{2}\)
Chu vi tam giác MAB là:
\(C_{MAB}=MA+MB+AB=\dfrac{3}{2}+3\sqrt{5}+\dfrac{3\sqrt{17}}{2}\)
Xét ΔMAB có \(cosAMB=\dfrac{MA^2+MB^2-AB^2}{2\cdot MA\cdot MB}=\dfrac{9}{\sqrt{85}}\)
=>\(sinAMB=\sqrt{1-\left(\dfrac{9}{\sqrt{85}}\right)^2}=\dfrac{2}{\sqrt{85}}\)
Diện tích tam giác MAB là:
\(S_{AMB}=\dfrac{1}{2}\cdot MA\cdot MB\cdot sinAMB=\dfrac{1}{2}\cdot\dfrac{3\sqrt{17}}{2}\cdot3\sqrt{5}\cdot\dfrac{2}{\sqrt{85}}\)
\(=\dfrac{9}{2}\)