Ta có:
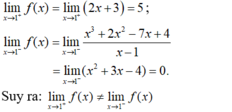
⇒ hàm số không liên tục tại x = 1 nên hàm số không có đạo hàm tại x0 = 1.
Chọn D.
Ta có:
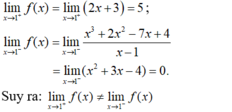
⇒ hàm số không liên tục tại x = 1 nên hàm số không có đạo hàm tại x0 = 1.
Chọn D.
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ±2.
B. k ≠ 2.
C. k ≠ -2.
D. k ≠ ±1.
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1
Cho hàm số f ( x ) = ( x + 1 ) 2 , x > 1 x 2 + 3 , x < 1 k 2 x = 1 . Tìm k để f(x) gián đoạn tại x= 1.
A. K ≢ ± 2
B. K ≢ 2
C. K ≢ - 2
D. K ≢ ± 1
1. đạo hàm của hàm số f(x) = 2x - 5 tại \(x_0=4\)
2. đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
3. đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Cho hàm số f ( x ) = 4 - x 2 - 2 ≤ x ≤ 2 1 x > 2 . Tìm khẳng định đúng trong các khẳng định sau:
(I) f(x) không xác định tại x = 3
(II) f(x) liên tục tại x = -2
(III) lim x → 2 f ( x ) = 2
A. Chỉ (I).
B. Chỉ (I) và (II).
C. Chỉ (I) và (III).
D. Cả (I); (II); (III) đều sai.
1) đạo hàm của hàm số \(y=x^2-3\sqrt{x}+\dfrac{1}{x}\)
2) đạo hàm của hàm số \(f\left(x\right)=\dfrac{x+9}{x+3}+4\sqrt{x}\) tại điểm x = 1
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
Cho hàm số f ( x ) có đạo hàm f ' ( x ) = ( x + 1 ) 4 ( x - 2 ) 5 ( x + 3 ) 3 . Số điểm cực trị của hàm số f ( x ) là:
A. 5
B. 3
C. 1
D. 2
1) cho hàm số \(f\left(x\right)=\dfrac{1}{3}x^3-2\sqrt{2}x^2+8x-1\) có đạo hàm là f'(x). Tập hợp những giá trị của x để f'(x) = 0
2) cho hàm số \(f\left(x\right)=\dfrac{3-3x+x^2}{x-1}\) giải bất phương trình f'(x) = 0
Cho hàm số f x = x + 1 2 , x > 1 x 2 + 3 , x < 1 k 2 , x = 1 . Tìm k để f(x) gián đoạn tại x = 1.
A. k ≠ ± 2
B. k ≠ 2
C. k ≠ - 2
D. k ≠ ± 1