Trong mặt phẳng Oxy cho đường thẳng d có phương trình 6x + 5y - 7 = 0; điểm I(2;-1). Phép đối xứng tâm I biến d thành d’ có phương trình:
A. 6x - 5y - 7 = 0
B. 6x + 5y - 7 = 0
C. 6x - 5y + 7 = 0
D. 6x + 5y + 7 = 0
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình: 3x - 5y + 7 = 0; đường thẳng d’ có phương trình 3x - 5y + 12 = 0. Một tâm đối xứng của (H) là:
A. (1;2)
B. (-4;0)
C. (0;19/10)
D. (19/10;0)
Hai đường thẳng d và d’ song song. Điểm A(1; 2) thuộc d và điểm B(-4; 0) thuộc d’ nên bị loại
Tính khoảng cách từ C tới hai đường thẳng d, d’
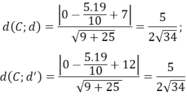
⇒ d(C;d)=d(C;d')=> C là tâm đối xứng
Nhận xét: nếu I là tâm đối xứng của hình gồm hai đường thẳng song song thì I cách đều hai đường thẳng song song đó.
Đáp án C
Trong mặt phẳng Oxy cho đường thẳng d có phương trình x − 5y + 7 = 0 và đường thẳng d’ có phương trình 5x – y – 13 = 0. Tìm phép đối xứng trục biến d thành d’.
Dễ thấy d và d' không song song với nhau.
Do đó trục đối xứng Δ của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'.
Từ đó suy ra Δ có phương trình:
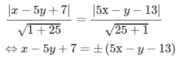
Từ đó tìm được hai phép đối xứng qua các trục:
Δ 1 có phương trình: x + y – 5 = 0,
Δ 2 có phương trình: x – y – 1 = 0.
Trong mặt phẳng Oxy cho hình (H) gồm đường thẳng d có phương trình 3x - 5y + 7 = 0 và đường thẳng d’ có phương trình:
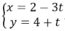
Tâm đối xứng của (H) là:
A. I(-7/2;7/2)
B. I(7;-7)
C. I(7/2;7/2)
D. I(7;7)
Đường thẳng d vó vecto chỉ phương u → = 5 ; 3 ; Đường thẳng d’ có vecto chỉ phương v → ( - 3 ; 1 ) nên d không song song với d’. Tâm đối xứng của hình (H) chính là giao điểm của d và d’:
Gọi I là giao điểm của d và d’.
Điểm I thuộc d’ nên tọa độ I(2- 3t; 4+ t)
Lại có, I thuộc d nên thay tọa độ điểm I vào phương trình đường thẳng d ta được:
3(2 - 3t) - 5(4 + t) + 7 = 0 ⇒ -14t = 7
⇒ t = − 1 2 ⇒ I 7 2 ; 7 2
Đáp án C
Trong mặt phẳng Oxy cho đường thẳng d có phương trình \(x-5y+7=0\) và đường thẳng d' có phương trình \(5x-y-13=0\). Tìm phép đối xứng trục biến d thành d' ?
Dễ thấy d và d' không song song với nhau. Do đó trục đối xứng \(\Delta\) của phép đối xứng biến d thành d' chính là đường phân giác của góc tạo bởi d và d'. Từ đó suy ra \(\Delta\) có phương trình :

Trong mặt phẳng Oxy cho đường thẳng d có phương trình 3x − 5y + 3 = 0 và vectơ v → = ( 2 ; 3 ) . Hãy viết phương trình đường thẳng d’ là ảnh của d qua phép tịnh tiến theo vectơ v → .
Gọi M′(x′;y′) ∈ d′ là ảnh của M(x,y) ∈ d qua phép tịnh tiến theo vecto v → ( 2 ; 3 )
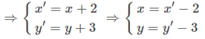
Do M(x,y) ∈ d nên
3x − 5y + 3 = 0
⇒ 3(x′−2) − 5(y′−3) + 3 = 0
⇔ 3x′ − 5y′ + 12 = 0 (d′)
Vậy M′(x′;y′) ∈ d′: 3x′ − 5y′ + 12 = 0
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình là 2 x + 5 y - 6 = 0 . Tìm tọa độ một vectơ chỉ phương u → của d.
A. u → = ( 2 ; 5 )
B. u → = ( 5 ; 2 )
C. u → = ( 5 ; - 2 )
D. u → = ( - 5 ; - 2 )
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d có phương trình là 2x+5y-6=0. Tìm tọa độ một vectơ chỉ phương u → của d.
![]()
![]()
![]()
![]()
Trong mặt phẳng Oxy, cho đường thẳng (d): 4x + y – 7 = 0. Đường thẳng đối xứng với (d) qua trục tung có phương trình:
A. 4x + y – 7 = 0
B. –4x + y – 7 = 0
C. 4x – y + 7 = 0
D. – 4x + y + 7 = 0
Đáp án C
x ' = − x y ' = y => – 4x + y – 7 = 0 => 4x – y + 7 = 0
Trong mặt phẳng Oxy, cho I(–2;1) và đường thẳng (d): 2x + 2y – 7 = 0. Ảnh của (d) qua phép đối xứng tâm I là đường thẳng có phương trình:
A. 2x + 2y – 11 = 0
B. 2x – 2y + 11 = 0
C. 2x + 2y + 11 = 0
D. –2x + 2y +11 =0
Đáp án C
Đ I : M(x;y) M’( – 4– x; 2– y)
=> 2 ( − 4 − x ) + 2 ( 2 − y ) − 7 = 0
⇒ ( d ' ) : 2 x + 2 y + 11 = 0