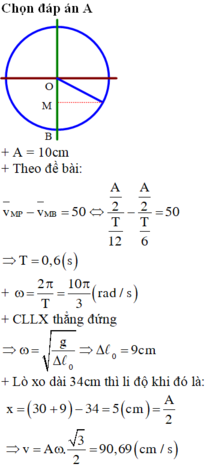b) Tìm điểm Mo (xo ; yo) thuộc đồ thị hàm số y=\(\frac{-2}{3}\)x biết: 5yo+2\(\left|x_o\right|\)=8

Những câu hỏi liên quan
Một con lắc lò xo gồm lò xo có độ cứng k 100N/m và vật nặng có khối lượng m 5/9 kg đang dao động điều hòa theo phương ngang với biên độ 2cm trên mặt phẳng nhẵn nằm ngang. Tại thời điểm m qua vị trí động năng bằng thế năng, một vật nhỏ có khối lượng mo 0,5m rơi thẳng đứng và dính chặt vào m. Khi qua vị trí cân bằng hệ (m + mo) có tốc độ bằng: A. 20cm/s. B. 30√3cm/s. C. 25cm/s. D. 5√12cm/s.
Đọc tiếp
Một con lắc lò xo gồm lò xo có độ cứng k = 100N/m và vật nặng có khối lượng m = 5/9 kg đang dao động điều hòa theo phương ngang với biên độ 2cm trên mặt phẳng nhẵn nằm ngang. Tại thời điểm m qua vị trí động năng bằng thế năng, một vật nhỏ có khối lượng mo = 0,5m rơi thẳng đứng và dính chặt vào m. Khi qua vị trí cân bằng hệ (m + mo) có tốc độ bằng:
A. 20cm/s.
B. 30√3cm/s.
C. 25cm/s.
D. 5√12cm/s.
Chọn A
+ Động năng bằng thế năng ở vị trí x = ±A√2/2 = ±√2 cm và v = ωA/√2 = 6π cm.
+ Khi mo rơi và dính vào m, theo định luật bảo toàn động lượng (chú ý là vật m0 rơi thẳng đứng nên động lượng của nó theo phương ngang = 0): (m+mo)v’ = mv => v’ = 4π cm/s.
+ Hệ (m + mo) có ω’ = 2π√3 rad/s và qua VTCB vận tốc của hệ là:
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Một lò xo nhẹ có chiều dài tự nhiên
ℓ
0
30
cm
được treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật có khối lượng m. Từ vị trí cân bằng O, kéo vật thẳng đứng xuống điểm B một đoạn OB 10cm rồi thả nhẹ cho vật dao động điều hòa. Gọi M là trung điểm của OB thì tốc độ trung bình của vật trên đoạn MB kém tốc độ trung bình của vật trên đoạn MO là 50cm/s. Cho
g
...
Đọc tiếp
Một lò xo nhẹ có chiều dài tự nhiên ℓ 0 = 30 cm được treo thẳng đứng, đầu trên cố định, đầu dưới gắn vật có khối lượng m. Từ vị trí cân bằng O, kéo vật thẳng đứng xuống điểm B một đoạn OB = 10cm rồi thả nhẹ cho vật dao động điều hòa. Gọi M là trung điểm của OB thì tốc độ trung bình của vật trên đoạn MB kém tốc độ trung bình của vật trên đoạn MO là 50cm/s. Cho g = 10 m / s 2 , lấy π 2 = 10 . Khi lò xo có chiều dài 34 cm, tốc độ của vật gần giá trị nào nhất?
A. 91cm/s
B. 74cm/s
C. 52cm/s
D. 105cm/s
Giả sử hàm số
y
f
x
có đạo hàm tại
x
o
. Hãy viết phương trình tiếp tuyến của đồ thị hàm số
g
f
x
có đạo hàm tại
x
o
. Hãy viết phương trình tiếp tuyến của đồ thị hàm số
g
...
Đọc tiếp
Giả sử hàm số y = f x có đạo hàm tại x o . Hãy viết phương trình tiếp tuyến của đồ thị hàm số g = f x có đạo hàm tại x o . Hãy viết phương trình tiếp tuyến của đồ thị hàm số g = f x tại M o x o ; f x o
Phương trình tiếp tuyến của đồ thị (C) của hàm số y = f(x) tại điểm Mo (xo;f(xo )) có dạng : y = f’(xo)(x – xo) + yo, trong đó yo = f(xo).
Đúng 0
Bình luận (0)
Xét đường thẳng (d) cổ định ở ngoài (0;R) (khoảng cách từ 0 đến (d) không nhỏ hơn R2). Từ một điểm M nằm trên đường thắng (d) ta dựng các tiếp tuyến MA, MB đến (O:R) ( A,B là các tiếp điểm) và dựng cát tuyên MCD (tia MC nằm giữa hai tia MO, MA và MC MD). Gọi E là trung điểm của CD, H là giao điểm của AB và MO. a, Chứng minh: 5 điểm M,A,E,O,B cùng nằm trên một đường tròn. b, Chứng minh: MC.MD MA² MO² –R² . c. Chứng minh: Các tiếp tuyến tại C,D của đường tròn (O;R) cắt nhau tại một điểm nằm trên...
Đọc tiếp
Xét đường thẳng (d) cổ định ở ngoài (0;R) (khoảng cách từ 0 đến (d) không nhỏ hơn R2). Từ một điểm M nằm trên đường thắng (d) ta dựng các tiếp tuyến MA, MB đến (O:R) ( A,B là các tiếp điểm) và dựng cát tuyên MCD (tia MC nằm giữa hai tia MO, MA và MC < MD). Gọi E là trung điểm của CD, H là giao điểm của AB và MO. a, Chứng minh: 5 điểm M,A,E,O,B cùng nằm trên một đường tròn. b, Chứng minh: MC.MD= MA² = MO² –R² . c. Chứng minh: Các tiếp tuyến tại C,D của đường tròn (O;R) cắt nhau tại một điểm nằm trên đường thắng AB. d. Chứng minh: Đường thắng AB luôn đi qua một điểm cố định. e, Chứng minh: Một đường thắng đi qua O vuông góc với MO cắt các tia MA, MB lần lượt tại PQ. Tìm GTNN của SMPO. Tìm vị trí điểm M để AB nhỏ nhất.
Trong mặt phẳng tọa độ Oxy cho điểm M(xo, yo).
a) Tìm tọa độ của điểm A đối xứng với M qua trục Ox;
b) Tìm tọa độ của điểm B đối xứng với M qua trục Oy;
c) Tìm tọa độ của điểm C đối xứng với M gốc O.
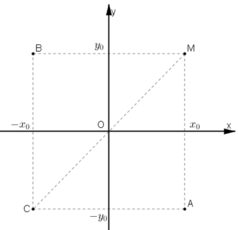
Biểu diễn các điểm trên hệ trục tọa độ ta thấy:
a) Điểm đối xứng với M(x0; y0) qua trục Ox là A(x0 ; –y0)
b) Điểm đối xứng với M(x0 ; y0) qua trục Oy là B(–x0 ; y0)
c) Điểm đối xứng với M(x0 ; y0) qua gốc O là C(–x0 ; –y0).
Đúng 0
Bình luận (0)
Tìm điểm M(xo,yo) thuộc đồ thị y=-2/3x bết 5yo+2|xo|=8
mot con lắc lò xo dao động điều hòa. Biết lò xo có độ cứng 36 N/m và vật nhỏ có khối lượng 100g. Lấy π²= 10. Động năng của con lắc biến thiên theo thời gian với tần số là
A.6Hz
B.1Hz
C.3 Hz
D.12Hz
Tìm a và b để các cực trị của hàm số
y
5
3
a
2
x
3
+
2
a
x
2
-
9
x
+
b
đều là nhưng số dương và
x
o
-
5
9
là điểm cực đại.
Đọc tiếp
Tìm a và b để các cực trị của hàm số y = 5 3 a 2 x 3 + 2 a x 2 - 9 x + b đều là nhưng số dương và x o = - 5 9 là điểm cực đại.
TXĐ: D = R.
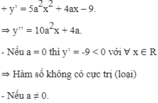
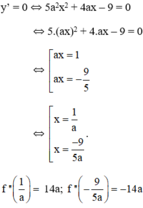
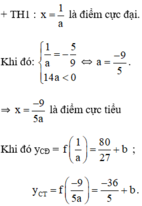
Các cực trị của hàm số đều dương
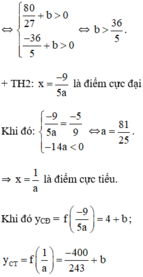
Các cực trị của hàm số đều dương
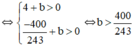
Vậy 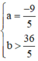 hoặc
hoặc 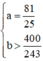 là các giá trị cần tìm.
là các giá trị cần tìm.
Đúng 0
Bình luận (0)
Hai lò xo giống nhau có chiều dài tự nhiên 50cm, độ cứng k = 50N / m, mắc vào hai điểm A, B và vật nặng m = 1 kg như hình vẽ. Khi vật nặng cân bằng, góc tạo bởi hai lò xo alpha = 100 ° lấy g=10 m/s^2
a. Tìm chiều dài của mỗi lò xo khi vật nặng cân bằng
b. Tìm khoảng cách giữa hai điểm A và B
Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, đọ cứng 50 N/ m, Khối lượng vật treo là 200 g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng hướng xuống dưới để lò xo giãn tổng cộng 12 cm rồi trả nhẹ cho nó dao động điều hòa. Lấy g10 (m/s2). Thời gian lực đàn hồi tác dụng lên vật cùng chiều với lực phục hồi trong một chu kỳ dao động là?
Đọc tiếp
Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, đọ cứng 50 N/ m, Khối lượng vật treo là 200 g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng hướng xuống dưới để lò xo giãn tổng cộng 12 cm rồi trả nhẹ cho nó dao động điều hòa. Lấy g=10 (m/s2). Thời gian lực đàn hồi tác dụng lên vật cùng chiều với lực phục hồi trong một chu kỳ dao động là?
Đề phải là: Một con lắc lò xo treo thẳng đứng, lò xo có khối lượng không đáng kể, độ cứng k = 50(N/m); khối lượng vật treo m = 200g. Vật đang đứng yên ở vị trí cân bằng thì được kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa. Lấy \(\pi^2=10;g=10\left(m,s^2\right)\). Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
Ta có: \(T=2\pi\sqrt{\dfrac{m}{k}}=0,4s\)
Tại VTCB lò xo giãn 1 đoạn bằng: \(\Delta l=\dfrac{mg}{k}=0,04m=4cm\)
Kéo thẳng đứng xuống dưới để lò xo giãn tổng cộng 12cm rồi thả cho nó dao động điều hòa =>A = 12 - 4 = 8 cm.
Trong một chu kỳ dao động thời gian lực đàn hồi tác dụng vào vật cùng chiều với lực hồi phục là:
t=T/2+T/3=5T/6=1/3s
Đúng 0
Bình luận (0)