Hai đường thẳng sau có vị trí tương đối là:
y=\(\dfrac{1}{2}\) x+5 ; y= -\(\dfrac{1}{2}\)x +5
Những câu hỏi liên quan
cho đường thẳng d1 : y = -2x+3 d2: y = -2x + m d3 : y = 1/2 x + 1 a) xét vị trí tương đối của hai đường thẳng d1 và d2 b) xét vị trí tương đối của hai đường thẳng d2 và d3
d1//d2 vì chung hệ số của x là -2
d2 cắt d3 do các hệ số a,b đều khác nhau
Đúng 1
Bình luận (0)
Hai đường thẳng
d
:
x
-
1
+
12
t
y
2
+
6
t
z
3
+...
Đọc tiếp
Hai đường thẳng d : x = - 1 + 12 t y = 2 + 6 t z = 3 + 3 t v à d ' : x = 7 + 8 t y = 6 + 4 t z = 5 + 2 t có vị trí tương đối là:.
A. Trùng nhau.
B. Song song.
C. Chéo nhau.
D. Cắt nhau.
d1 : y=-2x+3 , d2: y= -2x+m và d3; y=\(\dfrac{1}{2}x+1\)
Xét vị trí tương đối của hai đường thẳng:
a) d1 và d2 b) d2 và d3
Cho hai đường thẳng
d
1
:
x
−
2
2
y
−
1
z
+
3
2
và
d
2
:
x
−
1...
Đọc tiếp
Cho hai đường thẳng d 1 : x − 2 2 = y − 1 = z + 3 2 và d 2 : x − 1 = 2 y + 1 1 = 1 − z 1 . Phát biểu nào sau đây là đúng về vị trí tương đối của hai đường thẳng d 1 và d 2 .
A. d 1 / / d 2 .
B. d 1 ⊥ d 2 .
C. d 1 ≡ d 2 .
D. d 1 , d 2 chéo nhau và không vuông góc.
Đáp án A
Viết lại phương trình đường thẳng d 2 : x − 1 = y + 1 2 1 2 = z − 1 − 1 .
d 1 qua điểm A 2 ; 0 ; − 3 và có VTCP u 1 → = 2 ; − 1 ; 2 ;
d 2 qua điểm B 0 ; − 1 2 ; 1 và có VTCP u 2 → = − 1 ; 1 2 ; − 1 = − 1 2 2 ; − 1 ; 2 = − 1 2 u 1 → .
Mặt khác A 2 ; 0 ; − 3 ∉ d 2 .
Do đó d 1 / / d 2 .
Đúng 0
Bình luận (0)
Kết luận nào là đúng về vị trí tương đối của hai đường thẳng sau
d
1
:
x
+
y
+
2
z
0
x
−
y
+
z...
Đọc tiếp
Kết luận nào là đúng về vị trí tương đối của hai đường thẳng sau
d 1 : x + y + 2 z = 0 x − y + z + 1 = 0 và d 2 : x = − 2 + 2 t y = − t z = 2 + t
A. Hai đường thẳng vuông góc với nhau
B. Hai đường thẳng chéo nhau
C. Hai đường thẳng song song với nhau
D. Hai đường thẳng cắt nhau
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng
∆
1
:
x
-
1
1
y
2
z
-
3
-
1
và
∆
2
:
x
-...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz, xét vị trí tương đối của hai đường thẳng ∆ 1 : x - 1 1 = y 2 = z - 3 - 1 và ∆ 2 : x - 2 2 = y - 3 4 = z - 5 - 2
A. Trùng nhau
B. Song song
C. Chéo nhau
D. Cắt nhau
Trong không gian oxyz, cho hai đường thẳng d1:\(\left\{{}\begin{matrix}x=-1+3t\\y=-t\\z=1-2t\end{matrix}\right.\)và d2:\(\dfrac{x-1}{-3}=\dfrac{y-2}{1}=\dfrac{z-3}{3}\)Vị trí tương đối của d1 và d2 là
A. song song
B. trùng nhau
C. cắt nhau
D. chéo nhau
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: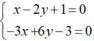 
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: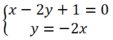 
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: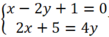 
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng
d
1
:
x
-
1
2
y
1
z
+
2
-
2
,
d
2
:
x
+...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho hai đường thẳng d 1 : x - 1 2 = y 1 = z + 2 - 2 , d 2 : x + 2 - 2 = y - 1 - 1 = z 2 . Xét vị trí tương đối của hai đường thẳng đã cho.
A. Chéo nhau
B. Trùng nhau
C. Song song
D. Cắt nhau
Ta có:
d 1 : x - 1 2 = y 1 = z + 2 - 2 có 1 véc tơ chỉ phương là: u 1 → 2 , 1 , - 2
d 2 : x + 2 - 2 = y - 1 - 1 = z 2 có 1 véc tơ chỉ phương là: u 2 → - 2 , - 1 , 2
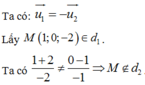
Vậy d 1 d 2 là hai đường thẳng song song
Chọn C
Đúng 0
Bình luận (0)