Hai số thực x; y thỏa mãn hệ điều kiện:
\(\left\{{}\begin{matrix}x^3+2y^2-4y+3=0\\x^2+x^2y^2-2y=0\end{matrix}\right.\)
Tính giá trị biểu thức: \(P=x^{2018}+y^{2019}\)
Cho x, y là hai số thực dương và m, n là hai số thực tùy ý. Đẳng thức nào sau đây là sai?
A. x n m = x n m
B. x m y n = x y m + n
C. x m x n = x m + n
D. x y n = x n y n
Cho hai số thực x,y. Chứng minh rằng nếu xy+x+y=-1 thì trong hai số x,y có ít nhất một số bằng -1
Ta có : xy + x + y = -1
=> x(y + 1) + y + 1 = -1 + 1
=> (x + 1)(y + 1) = 0
=> \(\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}\Rightarrow}\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\)(đpcm)
Vậy nếu xy + x + y = - 1 thì có ít nhất 1 số bằng - 1
xy + x + y = -1
<=> xy + x + y + 1 = 0
<=> x( y + 1 ) + 1( y + 1 ) = 0
<=> ( x + 1 )( y + 1 ) = 0
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\) ( đpcm )
\(xy+x+y=-1\)
\(< =>xy+x+y+1=0\)
\(< =>x\left(y+1\right)+\left(y+1\right)=0\)
\(< =>\left(x+1\right)\left(y+1\right)=0\)
\(< =>\orbr{\begin{cases}x+1=0\\y+1=0\end{cases}}\)
\(< =>\orbr{\begin{cases}x=-1\\y=-1\end{cases}}\)ez
Tìm số thực x để (x + căn bậc hai của 15) và (1/x - căn bậc hai của 15) đều là số nguyên.
Tìm tất cả các số thực x,y để hai số phức là hai số phức liên hợp của nhau.
A. ![]() .
.
B. ![]() .
.
C.![]() .
.
D.![]()
Để thực hiện phép tính tổng của hai số nguyên x và y ta thực hiện như sau :
A. Tong=x+y;
B. Tong:=x+y;
C. Tong:x+y;
D. Tong(x+y);
Cho x,y là hai số thực dương và m,n là 2 số thực tùy ý. Đẳng thức nào sau đây là sai?
A. x m . x n = x m + n
B. x m n = x m . n
C. x . y n = x n . y n
D. x m n = x m n
Đáp án D
Các đáp án A, B, C đều đúng, chỉ có D là sai.
Chọn phương án D.
Cho phương trình ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x 4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt
A. 3.
B. 4.
C. 5.
D. 6
Trong quá trình biến đổi và tính toán những biểu thức đại số, nhiều khi ta phải thực hiện phép nhân hai đa thức một biến, chẳng hạn ta cần thực hiện phép nhân sau:
\((x - 1)({x^2} + x + 1)\)
Làm thế nào để thực hiện được phép nhân hai đa thức một biến?
Muốn nhân một đa thức với một đa thức, ta nhân mỗi đơn thức của đa thức này với từng đơn thức của đa thức kia rồi cộng các tích với nhau.
Cho hàm số y=f(x) là hàm đa thức hệ số thực. Hình vẽ bên là đồ thị của hai hàm số y=f(x) và y=f'(x) . Phương trình f(x)= m e x có hai nghiệm thực phân biệt thuộc đoạn [0;2] khi và chỉ khi m thuộc nửa khoảng [a;b). Giá trị của a+b gần nhất với giá trị nào dưới đây ?
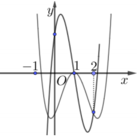
A. 0,27.
B. −0,54.
C. −0,27.
D. 0,54.
Cho phương trình ( x + x + 1 ) ( m x + 1 + 1 x + 16 x 2 + x 4 ) = 1 với m là tham số thực. Tìm số các giá trị nguyên của m để phương trình có hai nghiệm thực phân biệt.
![]()
![]()
![]()
![]()