Cho các hàm số y = 3x^2; y = - x^2
a) Vẽ đồ thị của các hàm số trên
b) Tính các giá trị f (- 3) ; f (7) ; f (6)
Những câu hỏi liên quan
Cho các hàm số sau:
y
1
x
−
3
I
;
y
x
3
−
3
x
+
2
I
I
;
y
−
x
4
+
2
x
2
...
Đọc tiếp
Cho các hàm số sau:
y = 1 x − 3 I ; y = x 3 − 3 x + 2 I I ; y = − x 4 + 2 x 2 I I I .
Trong các hàm số đã cho hàm không có cực trị là:
A. Chỉ (II)
B. Chỉ (III)
C. Chỉ (I)
D. (I) và (II)
Đáp án là C
• Hàm số (I) là hàm nhất biến nên không có cực trị.
• Hàm số (II) có phương trình y'=2 có 2 nghiệm phân biệt nên có 2 cực trị.
Hàm số (III) có a.b=-2<0 nên có 3 cực trị.
Đúng 0
Bình luận (0)
Cho các hàm số
y
x
+
1
x
−
1
;
y
x
4
+
2
x
2
+
2
;
y
−
x
3
+
x
2
−
3...
Đọc tiếp
Cho các hàm số y = x + 1 x − 1 ; y = x 4 + 2 x 2 + 2 ; y = − x 3 + x 2 − 3 x + 1. Trong các hàm số trên, có bao nhiêu hàm số đơn điệu trên ℝ ?
A. 3
B. 1
C. 2
D. 0
Đáp án C.
Ta có
y = − x 3 + x 2 − 3 x + 1 ⇒ y ' = − 3 x 2 + 2 x − 3 < 0 ; ∀ x ∈ ℝ
suy ra hàm số nghịch biến trên ℝ
Đúng 0
Bình luận (0)
Cho các hàm số y = 2 x 2 và y = -3x^2. Hỏi hàm số nào đồng biến khi x > 0
A. y = 2 x 2
B. y = -3 x 2
C. Không có hàm số nào
D. Cả hai
Đáp án A
Xét hàm số y = ax2 (a ≠ 0)
* Nếu a > 0 thì hàm số nghịch biến khi x < 0 và đồng biến khi x > 0.
* Nếu a < 0 thì hàm số đồng biến khi x < 0 và nghịch biến khi x > 0.
Do đó,chỉ có hàm số y = 2x2 đồng biến khi x> 0.
Đúng 0
Bình luận (0)
Từ đồ thị của hàm số y = 3 x , hãy vẽ đồ thị của các hàm số sau:
a) y = 3x – 2
b) y = 3x + 2
c) y = |3x – 2|
d) y = 2 – 3x
a) Đồ thị của hàm số y: y = 3 x − 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung xuống dưới 2 đơn vị (H. 49)
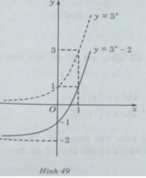
b) Đồ thị của hàm số y = 3 x + 2 nhận được từ đồ thị của hàm số y = 3 x bằng phép tịnh tiến song song với trục tung lên phía trên 2 đơn vị (H. 50)
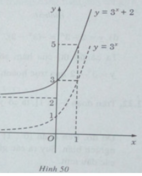
c)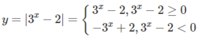 
Do đó, đồ thị của hàm số y = | 3 x − 2| gồm:
- Phần đồ thị của hàm số y = 3 x − 2 ứng với 3 x – 2 ≥ 0 (nằm phía trên trục hoành).
- Phần đối xứng qua trục hoành của đồ thị hàm số y = 3 x − 2 ứng với 3 x – 2 < 0.
Vậy đồ thị của hàm số y = | 3 x − 2| có dạng như hình 51.
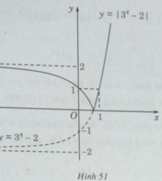
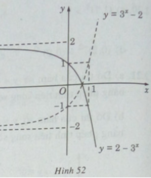
Ta có đồ thị của hàm số y = 2 − 3 x đối xứng với đồ thị cua hàm số y = 3 x – 2 qua trục hoành (H.52).
Đúng 0
Bình luận (0)
Cho hàm số y = 3x - 2
a) Xác định các hệ số a, b. Tìm hai điểm thuộc đồ thị hàm số trên
b) Tìm m để đường thẳng y = 3x - 2 cắt đường thẳng y = mx + 2
Bài 4. Cho các hàm số: y 3x và y -3x +41)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y -3x +4.4)Trong các điểm: C(dfrac{1}{3};3) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y -3x+4. Vì sao?5)Tìm trên đường thẳng y -3x+4 điểm có hoành độ bằng xdfrac{2}{3} .6) Tìm trên đường thẳng y -3x+4 điểm có tung độ bằng y -2 .7) Tìm trên đường thẳng y -3x +4 điể...
Đọc tiếp
Bài 4. Cho các hàm số: y =3x và y =-3x +4
1)Vẽ trên cùng hệ trục tọa độ, đồ thị hai hàm số đã cho.
2)Tìm tọa độ giao điểm M của đồ thị hai hàm số trên bằng phép toán.
3)Tính khoảng cách từ O ( gốc tọa độ) đến đường thẳng y =-3x +4.
4)Trong các điểm: C(\(\dfrac{1}{3};3\)) ; D(2;10) điểm nào thuộc, điểm nào không thuộc đồ thịhàm số y= -3x+4. Vì sao?
5)Tìm trên đường thẳng y =-3x+4 điểm có hoành độ bằng x=\(\dfrac{2}{3}\) .
6) Tìm trên đường thẳng y =-3x+4 điểm có tung độ bằng y = -2 .
7) Tìm trên đường thẳng y =-3x +4 điểm M (x;y) sao cho y2+ xy -2x2=0.
8) Tìm trên đường thẳng y =-3x+4 điểm N(x;y) sao cho khoảng cách từ N đến Ox bằng 4 lần khoảng cách từ N đến Oy
Cho các hàm số y=2x ; y = 3x + 3 và y= -2x+5
a) Vẽ đồ thị các hàm số trên cùng một hệ trục tọa độ. Tính số đo các góc tạo bởi đồ thị các hàm số trên với trục Ox.
b) Tính diện tích các tam giác tạo bởi mỗi đường thẳng y= 3x + 3 và y= -2x+5 với 2 trục tọa độ
cho hàm số y=x+3, y=-x-1, y=√3x -m-2. Tìm m để các đồ thị hàm số trên là các đường thẳng đồng quy
Trong các hàm số sau,hàm số nào là hàm số bậc nhất ? Với các hàm số bậc nhất , hãy cho biết hàm số đó đồng biến hay nghịch biến ?
a) y = 5 - 2x b) y = x√2 -1 c) y = 2(x+1) - 2x
d) y = 3(x-1) - x e) y = -2/3x f) y= x + 1/x
\(c,y=2x+2-2x=2\\ d,y=3x-3-x=2x-3\\ f,y=x+\dfrac{1}{x}=\dfrac{x^2+1}{x}\)
Hs bậc nhất là a,b,d,e
\(a,-2< 0\Rightarrow\text{nghịch biến}\\ b,\sqrt{2}>0\Rightarrow\text{đồng biến}\\ d,2>0\Rightarrow\text{đồng biến}\\ e,-\dfrac{2}{3}< 0\Rightarrow\text{nghịch biến}\)
Đúng 1
Bình luận (0)
Cho các phát biểu sau (1): Hàm số
y
x
3
+
3
x
2
+
3
x
+
1
có đồ thị là (C) không có cực trị (2).Hàm số
y
x
3
+
3
x
2
+
3
x
+
1
có điểm uốn là U(-1;0) (3). Đồ thị hàm số
y
3
x
-
2...
Đọc tiếp
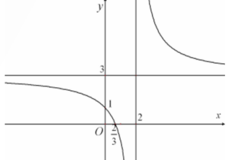
Cho các phát biểu sau (1): Hàm số y = x 3 + 3 x 2 + 3 x + 1 có đồ thị là (C) không có cực trị (2).Hàm số y = x 3 + 3 x 2 + 3 x + 1 có điểm uốn là U(-1;0) (3). Đồ thị hàm số y = 3 x - 2 x - 2 có dạng.Hàm số y = 2 x + 1 x + 1 có lim x → 1 + 2 x + 1 x + 1 = - ∞ và lim x → 1 - 2 x + 1 x + 1 = + ∞ .Số các phát biểu đúng là:
A. 1
B. 2
C. 3
D. 0
