Với x ≥ 0 ; x ≠ 9. Cho P=\(\dfrac{\sqrt{x}+3}{\sqrt{x}+8}\)
a. So sánh P với 1, so sánh P với 2
b. Với x ≥ 0 ; x ≠ 9. Chứng minh P>P2
c. Tìm x để 2P2<P
Mong các bạn giúp
Thanks
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |−5x| ta được biểu thức:
A. -5x với x > 0 và 5x với x < 0
B. -5x với x ≥ 0 và 5x với x < 0
C. 5x với x > 0 và -5x với x < 0
D. -5x với x ≤ 0 và 5x với x > 0
Khoanh tròn vào chữ cái trước khẳng định đúng.
Bỏ dấu giá trị tuyệt đối của biểu thức |x−2| ta được biểu thức:
A. x – 2 với x > 2 và 2 – x với x < 2
B. x – 2 với x ≥ 2 và 2 – x với x < 2
C. x – 2 với x > 0 và 2 – x với x < 0
D. x – 2 với x ≥ 0 và 2 – x với x < 0
Chứng minh rằng:
a) (x+1)2>=4x
b) x2+y2+2>=2(x+y)
c) (1/x+1/y)(x+y)>=4 (với x>0; y>0)
d) x/y+y/x>=2 ( với x>0; y>0)
Giúp mình với ạ <3
a) Giả sử `(x+1)^2 >= 4x` là đúng.
Có: `(x+1)^2 >=4x <=> x^2+2x+1>=4x`
`<=>x^2+1>=2x`
`<=>x^2-2x+1>=0`
`<=> (x-1)^2>=0 forall x`.
Vậy điều giả sử là đúng.
b) `x^2+y^2+2 >=2(x+y)`
`<=> (x^2-2x+1)+(y^2-2y+1) >=0`
`<=>(x-1)^2+(y-1)^2>=0 forall x,y`
c) `(1/x+1/y)(x+y)>=4`
`<=> (x+y)/(xy) (x+y) >=4`
`<=> (x+y)^2 >= 4xy`
`<=> x^2+2xy+y^2>=4xy`
`<=> (x-y)^2>=0 forall x,y > 0`
d) `x/y+y/x>=2`
`<=> (x^2+y^2)/(xy) >=2`
`<=> x^2+y^2 >=2xy`
`<=> (x-y)^2>=0 \forall x,y>0`.
a) Xét hiệu \(\left(x+1\right)^2-4x\) = \(x^2-2x+1=\left(x-1\right)^2\ge0\)
=> \(\left(x+1\right)^2-\text{4x}\) \(\ge\) 0
=> \(\left(x+1\right)^2\ge\text{4x}\) (điều phải chứng minh)
b) xét hiệu \(x^2+y^2+2-2\left(x+y\right)\) = \(\left(x-1\right)^2+\left(y-1\right)^2\ge0\)
=> \(x^2+y^2+2-2\left(x+y\right)\ge0\)
=> \(x^2+y^2+2\ge2\left(x+y\right)\) (điều phải chứng minh)
c) Xét hiệu \(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)-4\) = \((\dfrac{x+y}{xy})\left(x+y\right)-4=\dfrac{\left(x+y\right)^2-4xy}{xy}=\dfrac{\left(x-y\right)^2}{xy}\) \(\ge0\)(vì x>0,y>0)
=>\(\left(\dfrac{1}{x}+\dfrac{1}{y}\right)\left(x+y\right)\ge4\) (điều phải chứng minh)
d) Áp dụng bất đẳng thức Cau-Chy cho các số x>0;y>0 ta có
\(\dfrac{x}{y}+\dfrac{y}{x}\ge2.\left(\dfrac{xy}{yx}\right)=2\)
=> \(\dfrac{x}{y}+\dfrac{y}{x}\ge2\) (điều phải chứng minh)
Mình làm hơi tắt mong bạn thông cảm nhé
Chúc bạn học tốt
Mệnh đề phủ định của mệnh đề: "Với mọi số thực x, x² > 0" là
A. Với mọi số thực x, x² ≤ 0 B. Tồn tại số thực x, x² < 0
C. Tồn tại số thực x, x² ≤ 0 D. Với mọi số thực x, x² < 0
Trong các cặp hình phẳng giới hạn bởi các đường sau, cặp nào có diện tích bằng nhau?
a) {y = x + sinx, y = x với 0 ≤ x ≤ π} và {y = x + sinx, y = x với π ≤ x ≤ 2π}
b) {y = sinx, y = 0 với 0 ≤ x ≤ π} và {y = cosx, y = 0 với 0 ≤ x ≤ π};
c) {y = √x, y = x 2 }
và { 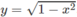 , y = 1 − x}
, y = 1 − x}
cho c E( thuộc ) Z so sánh ( -5 ) x(nhân) X với 0
với x<0 suy ra ( -5 ) x X ......0
với x> 0 suy ra ...................................................................
điền vào thôi
cho c E( thuộc ) Z so sánh ( -5 ) x(nhân) X với 0
với x<0 suy ra ( -5 ) x X ......0
với x> 0 suy ra ...................................................................
điền vào thôi
cho c E( thuộc ) Z so sánh ( -5 ) x(nhân) X với 0
với x<0 suy ra ( -5 ) x X ......0
với x> 0 suy ra ...................................................................
điền vào thôi
1. CMR
a) x^2-3x+5>0 với mọi x
b) x^2-1/3x+5/4>0 với mọi x
c)x-x^2-3<0 với mọi x
d) x-2x^2-5/2<0 với mọi x
hơi ngán dạng này :((((
a, \(x^2-3x+5=x^2-2.\frac{3}{2}x+\frac{9}{4}-\frac{9}{4}+5=\left(x-\frac{3}{2}\right)^2+\frac{11}{4}\ge\frac{11}{4}>0\forall x\)
b,
\(x^2-\frac{1}{3}x+\frac{5}{4}=x^2-2.\frac{1}{6}+\frac{1}{36}-\frac{1}{36}+\frac{5}{4}=\left(x-\frac{1}{6}\right)^2+\frac{11}{9}>0\forall x\)
c,
\(x-x^2-3=-\left(x^2-2.\frac{1}{2}x+\frac{1}{4}\right)+\frac{1}{4}-3=-\left(x-\frac{1}{2}\right)^2-\frac{11}{4}< 0\forall x\)d,
\(x-2x^2-\frac{5}{2}=-2\left(x^2-\frac{1}{2}x+\frac{5}{4}\right)=-2\left(x^2-2.\frac{1}{4}+\frac{1}{16}-\frac{1}{16}+\frac{5}{4}\right)=-2\left[\left(x-\frac{1}{4}\right)^2+\frac{19}{16}\right]=-2\left(x-\frac{1}{4}\right)^2-\frac{19}{8}< 0\forall x\)P/s : ko chắc lém :)))
Bài 1: Chứng minh
a. A = 2x ^ 2 + 2x + 1 > 0 với mọi x
b. B = 4 + x ^ 2 + x > 0 với mọi x
Bài 2: Chứng minh
a. A = - x ^ 2 + 3x - 1 < 0 với mọi x
b. B = - 2x ^ 2 - 3x - 3 < 0 với mọi x
Bài 1:
\(a,A=2x^2+2x+1=\left(x^2+2x+1\right)+x^2=\left(x+1\right)^2+x^2\\ Mà:\left(x+1\right)^2\ge0\forall x\in R\\ \Rightarrow\left(x+1\right)^2+x^2>0\forall x\in R\\ Vậy:A>0\forall x\in R\)
2:
a: =-(x^2-3x+1)
=-(x^2-3x+9/4-5/4)
=-(x-3/2)^2+5/4 chưa chắc <0 đâu bạn
b: =-2(x^2+3/2x+3/2)
=-2(x^2+2*x*3/4+9/16+15/16)
=-2(x+3/4)^2-15/8<0 với mọi x
Bài 1:
\(B=4+x^2+x=\left(x^2+x+\dfrac{1}{4}\right)+\dfrac{15}{4}=\left(x+\dfrac{1}{2}\right)^2+\dfrac{15}{4}\ge\dfrac{15}{4}\forall x\in R\\ Vậy:B>0\forall x\in R\)