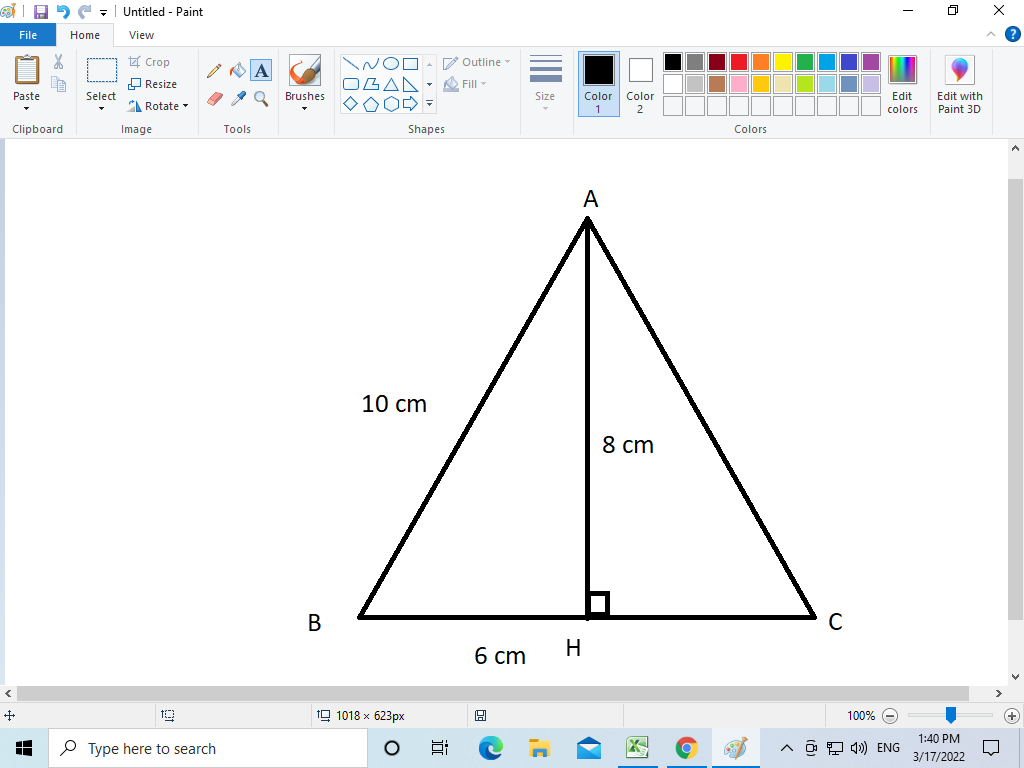
Cho tam giác ABC cân tại A, có AB = 10cm : BC= 16cm.Vẽ AH vuông góc BC tại A
a) CM ; tan giác HAB = tam giác HAC
b) CM: H là trung điểm BC. Tính AH
c) Vẽ HE vuông góc AB, HF vuông góc AC. CM ; tam giác HBE = tam giác HCF
d) CM; tam giác HAE = tam giác HAF và tam giác AEF cân