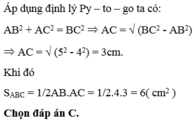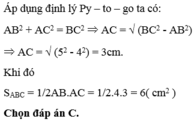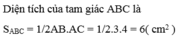Bài 22: Cho Δ ABC vuông tại A có AB= 10cm; góc ACB= 400
a) Tính độ dài BC
b) Kẻ tia phân giác BD của góc ABC (D ∈ AC). Tính AD?
Bài 23: Cho Δ ABC có AB= 12cm; góc B= 400, góc C= 300, đường cao AH. Hãy tính độ dài AH,HC
vẽ hình và giải chi tiết giúp mk vs ạ mk đang cần gấp cảm ơn mn nhìu