Cho hàm số y = f(x) = 4x2 - 5
a) Tính f(3) ; f (-1/2)
b) Tìm x để f(x) = (-1)
c) CMR: \(\forall\)x \(\varepsilon\)R thì f(x)=f(-x)
Cho hàm số y = f(x) = 4x2 - 5 a/ Tính f(3); b/ Tìm x để f(x) = -1 c/ Chứng tỏ rằng với x Î R thì f(x) = f(-x)
a) f(3) = 4.3^2 - 5 = 31
b) f(x) = -1
<=> 4x^2 - 5 = -1
<=> 4x^2 = 4
<=> x = 1 hoặc x = -1
c) f(x) = 4x^2 - 5 = 4(-x)^2 - 5 = f(-x)
cho hàm số y = f(x)=2x^2 -5
a) tính f(-2), f(1),f(3)
b) tính giá trị của x để f(x)=3
c) tìm x thuộc z sao cho f(x) âm
a) Thay x=-2 vào hàm số \(f\left(x\right)=2x^2-5\),ta được:
\(f\left(-2\right)=2\cdot\left(-2\right)^2-5=2\cdot4-5=8-5=3\)
Thay x=1 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(1\right)=2\cdot1^2-5=2-5=-3\)
Thay x=3 vào hàm số \(f\left(x\right)=2x^2-5\), ta được:
\(f\left(3\right)=2\cdot3^2-5=2\cdot9-5=18-5=13\)
Vậy: f(-2)=3
f(1)=-3
f(3)=13
b) Để f(x)=3 thì \(2x^2-5=3\)
\(\Leftrightarrow2x^2=8\)
\(\Leftrightarrow x^2=4\)
hay \(x\in\left\{2;-2\right\}\)
Vậy: Để f(x)=3 thì \(x\in\left\{2;-2\right\}\)
Bài 1: Cho hàm số y = f(x) = 4x2 - 5
a/ Tính f(3); )21(f−
b/ Tìm x để f(x) = -1
c/ Chứng tỏ rằng với x ∈ R thì f(x) = f(-x)
Cho hàm số y = f(x) = 4x2 – 9 a. Tính f(-2); f(-1/2) b. Tìm x để f(x) = -1 c. Chứng tỏ rằng với x thuộc R thì f(x) = f(-x)
Cho hàm số y=f(x)=4x² - 5
a) Tính f(3), f(-1/2)
b) Tìm x để f(x) = -1
c)Chứng tỏ với mọi x ∈ R thì f(x)= f(-x)
Giúp mình với ạ cẻm ưn nhiều:3
a) Ta có: \(y=f\left(x\right)=4x^2-5\)
\(\Rightarrow\left\{{}\begin{matrix}f\left(3\right)=4.3^2-5=31\\f\left(-\dfrac{1}{2}\right)=4.\left(-\dfrac{1}{2}\right)^2-5=-4\end{matrix}\right.\)
b) Ta có: \(f\left(x\right)=-1\)
\(\Rightarrow4x^2-5=-1\)
\(\Leftrightarrow4x^2=4\)
\(\Leftrightarrow x^2=1\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy \(x\in\left\{1;-1\right\}\) thì \(f\left(x\right)=-1\)
c) \(\forall x\in R,f\left(x\right)=f\left(-x\right)\Leftrightarrow f\left(-x\right)=4.\left(-x\right)^2-5=4x^2-5=f\left(x\right)\)
Vậy \(\forall x\in R\) thì \(f\left(x\right)=f\left(-x\right)\)
\(a.f\left(3\right)=4.3^2-5=31.\\ f\left(\dfrac{-1}{2}\right)=4.\left(\dfrac{-1}{2}\right)^2-5=-4.\)
\(b.f\left(x\right)=-1.\Rightarrow4x^2-5=-1.\\ \Leftrightarrow4x^2=4.\Leftrightarrow x^2=1.\\ \Leftrightarrow x=\pm1.\)
\(c.f\left(x\right)=f\left(-x\right).\\ \Rightarrow4x^2-5=4\left(-x\right)^2-5.\\ \Leftrightarrow4x^2-5=4x^2-5.\)
\(\Leftrightarrow0x=0\) (luôn đúng).
Vậy với mọi x ∈ R thì f (x)= f (-x).
a) Do \( y=f(x)=4x² - 5 \) nên :
\(+) f(3) = 4 . 3^2 - 5 = 4 . 9 - 5 = 36 - 5 = 31 \)
\(+) f(\dfrac{1}{2}) = 4 . (\dfrac{1}{2})^2 - 5 = 4 . \dfrac{1}{4} - 5 = 1 - 5 = -4 \)
Vậy : \(f(3) = 31 ; f(\dfrac{1}{2}) = -4 \)
b) Do \(f(x) = -1 \)
Mà \(f(x) = 4x^2 - 5 \)
\(=> \) \(4x^2 - 5 = -1 \)
\(=> 4x^2 = -1 + 5 \)
\(=> 4x^2 = 4 \)
\(=> x^2 = 1 \) \(= 1^2 = ( -1)^2 \)
\(=> x \) ∈ { -1 ; 1 }
Vậy với \(f(x) = -1 \) thì x ∈ { -1 ; 1 }
c) Ta có : Do \(x^2 = ( -x )^2 \)
\(=> \) \(4x^2 = 4(-x)^2 \)
\(=> 4x^2 - 5 = 4( -x )^2 - 5 \)
\(=> f(x) = f(-x) \)
Vậy với mọi x ∈ R thì \(f(x) = f(-x)\)
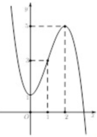
Cho hàm số y = f ( x ) là hàm đa thức bậc 4, có đồ thị hàm số y = f ' ( x ) như hình vẽ.

Hàm số y = f ( 5 − 2 x ) + 4 x 2 − 10 x đồng biến trong các khoảng nào sau đây?
A. ( 3 ; 4 ) .
B. 2 ; 5 2 .
C. 3 2 ; 2 .
D. 0 ; 3 2 .
Cho hàm số y=f(x) có đạo hàm liên tục trên ( 0 ; + ∞ ) thỏa mãn f ' ( x ) + f ( x ) x = 4 x 2 + 3 x và f(1)=2. Phương trình tiếp tuyến của đồ thị hàm số y=f(x) tại điểm có hoành độ x = 2 là x
A. y = 16x+20.
B. y = -16x+20
C. y = -16x-20
D. y = 16x-20.
Cho y=f(x) là hàm đa thức bậc 4, có đồ thị hàm số y=f '(x) như hình vẽ bên . Hàm số y = f ( 5 - 2 x ) + 4 x 2 - 10 x đồng biến trên khoảng nào dưới đây?
A. (3;4)
B. 2 ; 5 2
C. 3 2 ; 2
D. 0 ; 3 2
Ta có ![]()
![]()
Đặt ![]() bất phương trình trở thành:
bất phương trình trở thành: ![]()
Kẻ đường thẳng y=5-2x qua các điểm (0;5), (1;3) nhận thấy t ∈ 0 ; 1 thì f '(t)<5-2t
Khi đó ![]()
Chọn đáp án B.
Gọi M là giá trị lớn nhất của(x hàm số y = f(x) = 4 x 2 - 2 x + 3 + 2 x - x 2 . Tính tích các nghiệm của phương trình f(x) = M
A. -1
B. 0
C. 1
D. 2
Đáp án A
Phương pháp: Đặt ![]()
![]()
Cách giải: Đặt ![]()
![]()
Khi đó ta có ![]()
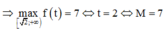
![]()
Khi đó tích hai nghiệm của phương trình này bằng -1
Cho hàm số y=f(x)=-5x
Chứng minh:
a) Hàm số là hàm số nghịch biến
b) f(x1+4x2)=f(x1)+4f(x2)
c) -f(x)=f(-x)
Cái này nhớ không nhầm là toán 7 :>
a) Gọi x1 và x2 là hai gtrị tương ứng của x
Giả sử x1<x2
Vì y=f(x) =-5x
\(\Rightarrow\)f(x1)=-5x1
\(\Rightarrow\)f(x2)=-5x2
mà x1<x2 \(\Rightarrow\)f(x1)>f(x2)
\(\Rightarrow\)Hs là hs nghịch biến
b) Vì y=f(x)=-5x
\(\Rightarrow\)f(x1)+4f(x2)
=-5x1+4(-5)x2
=-5(x1+4x2) (*)
\(\Rightarrow\)f(x1+4x2)=-5(x1+4x2) (**)
Từ (*), (**) \(\Rightarrow\)f(x1+4x2)=f(x1)+4f(x2)
c) Vì y=f(x)=-5x
\(\Rightarrow\)-f(x)=5x (*)
\(\Rightarrow\)f(-x)=-5(-x) =5x (**)
Từ (*) và (**) \(\Rightarrow\)-f(x) =f(-x)