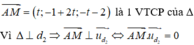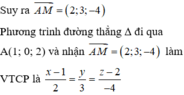Cho các đường thẳng d1: x+y-1=0 ; d3: y=3-2x d2: y=-2x+1 ; d4: 2y=x+4 a, Hãy chỉ ra các cặp đường thẳng song song, các cặp đường thẳng cắt nhau. b, Vẽ các đường d1, d2, d3 trên cùng 1 hệ trục toạ độ.

Những câu hỏi liên quan
Cho hai đường thẳng (d1 ) : y = (m +1)x + m+3 và (d2 ) : y= (2m+1)x-m+3 với m khác 0. Tìm tất cả các giá trị m (m khác 0) để (d1) và (d1) cắt nhau tại điểm M sao cho M nằm trên đường thẳng (d): y=x
Cho các đường thẳng
d
1
:
x
−
1
1
y
+
1
2
z
−
1
và
d
2
:
x
−
2
1...
Đọc tiếp
Cho các đường thẳng d 1 : x − 1 1 = y + 1 2 = z − 1 và d 2 : x − 2 1 = y 2 = z + 3 2 . Viết phương trình đường thẳng ∆ đi qua A (1; 0; 2), cắt d 1 và vuông góc với d 2 .
A. x − 1 2 = y − 2 = z − 2 1
B. x − 1 4 = y − 1 = z − 2 − 1
C. x − 1 2 = y 3 = z − 2 − 4
D. x − 1 2 = y − 2 = z − 2 1
Cho các đường thẳng
d
1
:
x
-
1
1
y
+
1
2
z
-
1
và
d
2
:...
Đọc tiếp
Cho các đường thẳng d 1 : x - 1 1 = y + 1 2 = z - 1 và d 2 : x - 2 1 = y 2 = z + 3 2 . Viết phương trình đường thẳng D đi qua A (1; 0; 2), cắt d1 và vuông góc với d2.
![]()
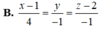
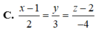
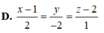
Cho hai đường thẳng d1 : x+ y -1= 0 và d2 : x- 3y + 3= 0. Phương trình đường thẳng d đối xứng với d1 qua đường thẳng d2 là:
A.x-7y +1 =0
B.x+7y +1= 0
C. 7x+y+1= 0
D. 7x-y+1= 0
Đáp án D
+Giao điểm của d1 và d2 là nghiệm của hệ
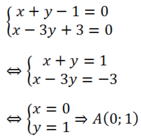
+Lấy M(1 ; 0) thuộc d1. Tìm M’ đối xứng M qua d2
+Viết phương trình đường thẳng ∆ đi qua M và vuông góc với d2 là
3(x-1) + 1( y=0) =0 hay 3x+ y-3= 0
Gọi H là giao điểm của ∆ và đường thẳng d2. Tọa độ H là nghiệm của hệ
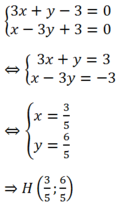
Ta có H là trung điểm của MM’. Từ đó suy ra tọa độ:
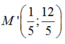
Viết phương trình đường thẳng d đi qua 2 điểm A và M’ : đi qua A(0 ;1) , vectơ chỉ phương 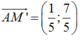
=> vectơ pháp tuyến 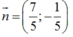
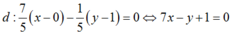
Đúng 1
Bình luận (1)
các đường thẳng sau có đồng quy không?
a) d1 : y = 3x + 1, d2 : y = -x và d3: y = x + 1/2
b) d1 : x + y - 1 = 0, d2 : y = 3x + 5 và d3 : x - 1/3y +5/3 = 0
trả lời đúng cho tích-kun
a, Hoành độ giao điểm d1 ; d2 thỏa mãn phương trình
\(3x+1=-x\Leftrightarrow4x+1=0\Leftrightarrow x=-\frac{1}{4}\)
\(\Rightarrow y=-\frac{3}{4}+1=\frac{1}{4}\)
Vậy d1 cắt d2 tại A(-1/4;1/4)
Để 3 điểm đồng quy khi d3 cắt A(-1/4;1/4) <=> \(\frac{1}{4}=-\frac{1}{4}+\frac{1}{2}\)( đúng )
Vậy 3 điểm đồng quy
b, d1 : \(y=1-x\)
Hoành độ giao điểm d1 ; d2 thỏa mãn phương trình
\(1-x=3x+5\Leftrightarrow4x=-4\Leftrightarrow x=-1\)
\(\Rightarrow y=-3+5=2\)
Vậy d1 cắt d2 tại T(-1;2)
Để 3 điểm đồng quy khi d3 cắt T(-1;2) <=> \(-1-\frac{2}{3}+\frac{5}{3}=0\)( luôn đúng )
Vậy 3 điểm đồng quy
Bài II (3,0 điểm) Cho 2 đường thẳng: (d1): y +2x 4 và (d2): y− +x 1 .1) Tìm tọa độ giao điểm A của đường thẳng (d1) và đường thẳng (d2).2) Xác định hệ số a, b của đường thẳng y ax b + (a0) biết đường thẳng đó song song với đường thẳng (d1) và đi qua điểm M (-1; 3). 3) Gọi B và C lần lượt là giao điểm của đường thẳng (d1) và (d2) với trục hoành. Tính diện tích tam giác ABC.
Đọc tiếp
Bài II (3,0 điểm) Cho 2 đường thẳng: (d1): y= +2x 4 và (d2): y=− +x 1 .
1) Tìm tọa độ giao điểm A của đường thẳng (d1) và đường thẳng (d2).
2) Xác định hệ số a, b của đường thẳng y ax b= + (a0) biết đường thẳng đó song song với đường thẳng (d1) và đi qua điểm M (-1; 3).
3) Gọi B và C lần lượt là giao điểm của đường thẳng (d1) và (d2) với trục hoành. Tính diện tích tam giác ABC.
1, PT hoành độ giao điểm: \(2x+4=-x+1\Leftrightarrow x=-1\Leftrightarrow y=0\)
\(\Leftrightarrow A\left(-1;0\right)\)
Vậy \(A\left(-1;0\right)\) là tọa độ giao điểm 2 đths
2, Đt cần tìm //(d1)\(\Leftrightarrow a=2;b\ne4\)
Đt cần tìm đi qua M(-1;3) nên \(-a+b=3\Leftrightarrow-2+b=3\Leftrightarrow b=5\left(tm\right)\)
Vậy đths là \(y=2x+5\)
3, PT giao điểm d1 với trục hoành là \(y=0\Leftrightarrow2x+4=0\Leftrightarrow x=-2\Leftrightarrow B\left(-2;0\right)\)
PT giao điểm d2 với trục hoành là \(y=0\Leftrightarrow-x+1=0\Leftrightarrow x=1\Leftrightarrow C\left(1;0\right)\)
Do đó \(BC=\left|-2\right|+\left|1\right|=3;OA=\left|-1\right|=1\)
Vậy \(S_{ABC}=\dfrac{1}{2}OA\cdot BC=\dfrac{3}{2}\left(đvdt\right)\)
Đúng 2
Bình luận (1)
Cho điểm A(1; 3) và hai đường thẳng
d
1
:
2
x
−
3
y
+
4
0
,
d
2
:
3
x
+
y
0
. Số đường thẳng qua A và tạo với
d
1
,
d
2
các góc bằng nhau là A.1 B.2 C.4 D.Vô số
Đọc tiếp
Cho điểm A(1; 3) và hai đường thẳng d 1 : 2 x − 3 y + 4 = 0 , d 2 : 3 x + y = 0 . Số đường thẳng qua A và tạo với d 1 , d 2 các góc bằng nhau là
A.1
B.2
C.4
D.Vô số
ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.
Đúng 0
Bình luận (0)
Cho điểm A(1; 1) và hai đường thẳng (
d
1
): y x − 1; (
d
2
): y 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), (
d
1
) tạo thành một tam giác vuông. A. y 2x–1 B. y –2x+3 C.
y
−
x
+...
Đọc tiếp
Cho điểm A(1; 1) và hai đường thẳng ( d 1 ): y = x − 1; ( d 2 ): y = 4x − 2. Viết phương trình đường thẳng (d) đi qua điểm A và cắt các đường thẳng (d1), ( d 1 ) tạo thành một tam giác vuông.
A. y = 2x–1
B. y = –2x+3
C. y = − x + 2 y = − 1 4 x + 5 4
D. Không xác định được
Cho ba đường thẳng
d
1
:
x
−
2
y
+
1
0
,
d
2
:
m
x
−
3
m
−
2
y
+
2
m
−
2
0
,
d
3
:
...
Đọc tiếp
Cho ba đường thẳng d 1 : x − 2 y + 1 = 0 , d 2 : m x − 3 m − 2 y + 2 m − 2 = 0 , d 3 : x + y − 5 = 0 . Giá trị m để hai đường thẳng d1;d2 cắt nhau tại một điểm nằm trên d3 là
A.m = 0
B.m = 1
C.m = 2
D. không tồn tại m thỏa mãn
Để hai đường thẳng d1; d2 cắt nhau tại một điểm nằm trên d3 khi và chỉ khi 3 đường thẳng d1; d2; d3 đồng quy.
Giao điểm của d1 và d3 là nghiệm hệ phương trình:
x − 2 y + 1 = 0 x + y − 5 = 0 ⇔ x = 3 y = 2 ⇒ A ( 3 ; 2 )
Do 3 đường thẳng này đồng quy nên điểm A thuộc d2. Suy ra:
3m - (3m-2).2 + 2m – 2= 0
⇔ 3m – 6m + 4 + 2m – 2 = 0 ⇔ - m + 2 = 0 ⇔ m= 2
Với m= 2 thì đường thẳng d2 : 2x - 4y + 2= 0 hay x- 2y + 1 =0 . Khi đó, đường thẳng d1 và d2 trùng nhau.
Vậy không có giá trị nào của m thỏa mãn.
ĐÁP ÁN D
Đúng 0
Bình luận (0)