Để đo chiều rộng AB của một khúc sông người ta dựng được ba điểm C, D, E thẳng hàng; ba điểm C, B, A thẳng hàng và BD song song với AE . Biết rằng CB = 34 m, CD = 32m, CE = 100 m. Tìm chiều rộng AB của khúc sông đó

Những câu hỏi liên quan
Bài 4 : ( 1,5 điểm ) : Để đo chiều rộng của một con sông AB , người ta có thể đặt hai cọc tiêu ở vị trí EF sao cho EF / AB . Chọn 1 vị trí đứng ngắm ( điểm C ) sao cho ba điểm B , E , C thẳng hàng ; ba điểm A , F , C thẳng hàng . Đo được CF = 4m , AF = 6m ; EF = 6M . Hỏi khúc sông AB đó rộng bao nhiêu mét ?
Xét ΔCAB có FE//AB
nên FE/AB=CF/CA
=>6/AB=4/10=2/5
=>AB=15(m)
Đúng 0
Bình luận (0)
giá cây cầu AB bắc qua một con sông có chiều rộng 300m .Người ta chọn điểm E trên đường thẳng AB sao cho điểm E,C,D thẳng hàng.Trên mặt đất người ta đo được AE=400m EC=500m tính khoảng cách giữa C và D
Để đo chiều rộng AB của 1 khúc sông mà ko phải băng qua nó, người ta xác định điểm C sao cho AC 60m. Từ C nhìn thấy B một góc ACB theo phương bằng 50 độ. Tính chiều rộng khúc sông ( Kết quả làm tròn đến chữ số thập phân thứ 2)
Đọc tiếp
Để đo chiều rộng AB của 1 khúc sông mà ko phải băng qua nó, người ta xác định điểm C sao cho AC= 60m. Từ C nhìn thấy B một góc ACB theo phương bằng 50 độ. Tính chiều rộng khúc sông ( Kết quả làm tròn đến chữ số thập phân thứ 2)
Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m
Đúng 1
Bình luận (0)
Để đo chiều rộng AB của 1 khúc sông mà ko phải băng qua nó, người ta xác định điểm C sao cho AC= 60m. Từ C nhìn thấy B một góc ACB theo phương bằng 50 độ. Tính chiều rộng khúc sông ( Kết quả làm tròn đến chữ số thập phân thứ 2)
Ta có:
tan C = AB/AC
AB = AC.tan C
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng khúc sông là 71,51 m
Đúng 0
Bình luận (0)
Để đo chiều rộng AB của 1 khúc sông mà ko phải băng qua nó, người ta xác định điểm C sao cho AC= 60m. Từ C nhìn thấy B một góc ACB theo phương bằng 50 độ. Tính chiều rộng khúc sông ( Kết quả làm tròn đến chữ số thập phân thứ 2)
Ta có:
tan ACB = AB/AC
⇒ AB = AC.tan ACB
= 60.tan 50⁰
≈ 71,51 (m)
Vậy chiều rộng của khúc sông là 71,51 m
Đúng 0
Bình luận (0)
để đo chiều cao AB của một tòa nhà người ta đặt một dụng cụ đo đạc NM thẳng đứng trên mặt đất và xác định được điểm C trên mặt đất sao cho ba điểm A,N,C thẳng hàng và ba điểm B,M,C thẳng hàng. Biết rằng NM=1,5 m, CN=1,25m,CA=20 m
Tính chiều cao AB của tòa nhà đó
Mình đang cần gấp
Ta có: NM//AB
=> \(\dfrac{NM}{AB}=\dfrac{CN}{AC}< =>AB=1,5\cdot\dfrac{20}{1,25}=24\left(m\right)\)
Vậy tòa nhà đó cao 24m
Đúng 1
Bình luận (1)
2. Để đo chiều rộng AB của một khúc sông mà không phải băng ngang qua nó, một người đi từ A đến C đo được AC = 50m và từ C nhìn thấy B với góc nghiêng 62° với bờ sông. Tính bề rộng của khúc sông( làm tròn đến mét )
Để đo chiều cao AB của một tòa nhà người ta đặt một dụng cụ đo đạc NM thẳng đứng trên mặt đất và xác định được điểm C trên mặt đất sao cho ba điểm A, N, C thẳng hàng và ba điểm B, M, C thẳng hàng (xem hình vẽ). Biết rằng NM = 1,5 m, CN = 1,25 m, CA = 20 m.
Tính chiều cao AB của tòa nhà đó. help em với mn ơi
Ta có :
\(\dfrac{NM}{AB}\) và \(\dfrac{CN}{CA}\) .
Vì \(\dfrac{NM}{AB}\) = \(\dfrac{CN}{CA}\) \(\Leftrightarrow\) AB = 1,5 . \(\dfrac{20}{1,25}\) = 24 ( m ) .
Vậy chiều cao AB của tòa nhà đó là 24 m .
Đúng 1
Bình luận (0)
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không? Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB x theo BC a, B’C’ a’; BB’ h.
Đọc tiếp
Có thể đo được chiều rộng của một khúc sông mà không cần phải sang bờ bên kia hay không?
Người ta tiến hành đo đạc các yếu tố hình học cần thiết để tính chiều rộng của khúc sông mà không cần phải sang bờ bên kia. Nhìn hình vẽ đã cho, hãy mô tả những công việc cần làm và tính khoảng cách AB =x theo BC =a, B’C’ = a’; BB’ = h.
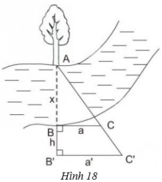
+ Mô tả cách làm:
- Chọn một điểm A cố định bên mép bờ sông bên kia (chẳng hạn như là một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn lại và AB chính là khoảng cách cần đo.
- Trên hai đường thẳng vuông góc với AB' tại B và B' lấy C và C' thằng hàng với A.
- Đo độ dài các đoạn BB' = h, BC = a, B'C' = a' ta sẽ tính được đoạn AB.
+ Cách tính AB.
Ta có: BC ⊥ AB’ và B’C’ ⊥ AB’ ⇒ BC // B’C’
ΔAB’C’ có BC // B’C’ (B ∈ AB’, C ∈ AC’)
⇒ 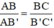 (hệ quả định lý Talet)
(hệ quả định lý Talet)
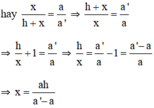
Đúng 0
Bình luận (0)

















