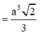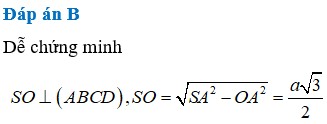cho hình chóp S.ABCD; ABCD là hình vuông cạnh 2a; SA vuông góc với ABCD; SA = a căn 2. Kẻ AH vuôgn góc với Sb; AK vuông góc với SD. Chứng minh rằng: a) BC vuông góc SAB; b) BD vuông góc SAC; c) AH vuông góc SBC; d) SC vuông góc với AKH

Những câu hỏi liên quan
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhấtA. ba điểm phân biệtB. 1 điểm và 1 đường thẳngC. 2 đường thẳng cắt nhauD. 4 đ...
Đọc tiếp
1. cho hình chóp S.ABCD có đáy ABCD là hình vuông. Số mặt bên của hình chóp là? Kể tên
2. cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật. Số cạnh đáy của hình chóp là? Kể tên
3. cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Vị trí tương đối giữa 2 đường thẳng SA và BC là
4. hình tứ diện ABCD có bao nhiêu đỉnh? Kể tên
5. hình chóp S.ABCD có bao nhiêu mặt. Kể tên
6. các yếu tố nào sau đây xác định 1 mặt phẳng duy nhất
A. ba điểm phân biệt
B. 1 điểm và 1 đường thẳng
C. 2 đường thẳng cắt nhau
D. 4 điểm phân biệt
1: Số mặt bên là 4
\(SAB;SAD;SBC;SCD\)
2: Số cạnh đáy là 4
AB,BC,CD,DA
3: SA và BC là hai đường thẳng chéo nhau
4: 4 đỉnh: A,B,C,D
5: Có 7 mặt: \(SAB;SAD;SBC;SCD;SAC;SBD;ABCD\)
6C
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36 c m 3 . Tính độ dài đường cao của hình chóp?
A. 6( cm )
B. 8( cm )
C. 5,4( cm )
D. 7,2( cm )
Áp dụng công thức thể tích của hình chóp ta có: V = 1 3 . h . S A B C D
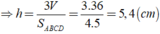
Chọn đáp án C.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA
⊥
(ABCD). Tính thể tích V của khối chóp S.ABCD.
A
.
V
a
2
3
2
B
.
V
a
3
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA ⊥ (ABCD). Tính thể tích V của khối chóp S.ABCD.
A . V = a 2 3 2
B . V = a 3 2 6
C . V = a 3 2
D . V = a 3 3 3
Cho hình chóp S.ABCD có đáy là hình chữ nhật ABCD có AB = 4cm,BC = 5cm. Biết thể tích của hình chóp S.ABCD bằng 36 ( c m 3 ) . Tính độ dài đường cao của hình chóp?
A. 6( cm )
B. 8( cm )
C. 5,4( cm )
D. 7,2( cm )
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AB 2a, BC a. Các cạnh bên của hình chóp đều bằng nhau và bằng
a
2
. Thể tích hình chóp S.ABCD bằng A.
a
3
3
2
B.
a
3...
Đọc tiếp
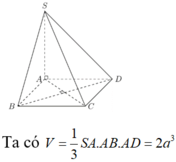
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AB = 2a, BC = a. Các cạnh bên của hình chóp đều bằng nhau và bằng a 2 . Thể tích hình chóp S.ABCD bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 4
D. a 3 3 5
Đáp án B
Dễ chứng minh
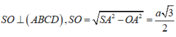
⇒ V c h o p = 1 3 S O . S A B C D = a 3 3 3
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AB2a, BCa. Các cạnh bên của hình chóp đều bằng nhau và bằng
a
2
. Thể tích hình chóp S.ABCD bằng A.
a
3
3
2
B.
a
3
3
3
C. ...
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật tâm O với AB=2a, BC=a. Các cạnh bên của hình chóp đều bằng nhau và bằng a 2 . Thể tích hình chóp S.ABCD bằng
A. a 3 3 2
B. a 3 3 3
C. a 3 3 4
D. a 3 3 5
Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tính thể tích V của hình chóp S.ABCD biết ABa, AD3a, SA2a. A. V3a3 B. V2a3 C. Va3 D. V6a3.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình chữ nhật. Tính thể tích V của hình chóp S.ABCD biết AB=a, AD=3a, SA=2a.
A. V=3a3
B. V=2a3
C. V=a3
D. V=6a3.
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy,
S
A
a
3
. Tính thể tích hình chóp S.ABCD A.
a
3
3
B.
a
3
3
3
C....
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 3 . Tính thể tích hình chóp S.ABCD
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy,
S
A
a
3
. Tính thể tích hình chóp S.ABCD A.
a
3
3
B.
a
3
3
3
C.
a
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a, SA vuông góc với đáy, S A = a 3 . Tính thể tích hình chóp S.ABCD
A. a 3 3
B. a 3 3 3
C. a 3 3
D. 3 a 3 3
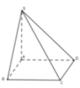
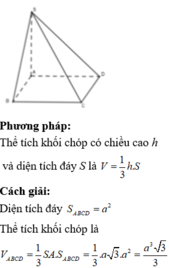
Diện tích đáy S A B C D = a 2
Thể tích khối chóp là
V A B C D = 1 3 S A . S A B C D = 1 3 . a 3 . a 2 = a 3 3 3
Chọn đáp án B.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, SA vuông góc với đáy. Tâm mặt cầu ngoại tiếp hình chóp S.ABCD là
A. Trung điểm cạnh SD.
B. Trung điểm cạnh SC.
C. Giao điểm của hai đường chéo AC và BD
D. Trọng tâm tam giác SAC.