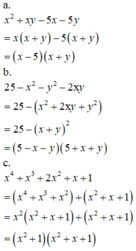Cho các đa thức: P(x) = x4 - 5x + 2x2 + 1; Q(x) = 5x + x2 + 5 - 3x2 + x4
a) Tìm M(x) = P(x) + Q(x).
b) Chứng tỏ M(x) không có nghiệm.

Những câu hỏi liên quan
. Cho các đa thức: P(x) = x4 - 5x + 2x2 + 1; Q(x) = 5x + x2 + 5 - 3x2 + x4
a) Tìm M(x) = P(x) + Q(x).
b) Chứng tỏ M(x) không có nghiệm.
`M(x)=P(x)+Q(x)`
`=x^4-5x+2x^2+1+5x+x^2+5-3x^2+x^4`
`=2x^4+6`
Đặt `M(x)=0`
`<=>2x^4+6=0`
`<=>x^4=-3`(vô lý vì `x^4>=0`)
Đúng 1
Bình luận (0)
Cho hai đa thức
A
(
x
)
x
5
+
x
2
+
5
x
+
6
-
x
5
-
3
x
-
5
,
B
(
x
)
x
4
+
2
x...
Đọc tiếp
Cho hai đa thức
A ( x ) = x 5 + x 2 + 5 x + 6 - x 5 - 3 x - 5 , B ( x ) = x 4 + 2 x 2 - 3 x - 3 - x 4 - x 2 + 3 x + 4
a. Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm dần của biến.
a. Ta có: A(x) = x5 + x2 + 5x + 6 - x5 - 3x - 5
= x2 + 2x + 1 (0.5 điểm)
B(x) = x4 + 2x2 - 3x - 3 - x4 - x2 + 3x + 4 = x2 + 1 (0.5 điểm)
Đúng 0
Bình luận (0)
Cho các đa thức P(x) = x – 2x2 + 3x5 + x4 + x – 1
và Q(x) = 3 – 2x – 2x2 + x4 – 3x5 – x4 + 4x2
a) Thu gọn và sắp xếp các đa thức trên theo lũy thừa giảm của biến.
b) Tính a/ P(x) + Q(x)b/ P(x) – Q(x).
Phân tích các đa thức sau thành nhân tửa)
x
2
+
x
y
−
5
x
−
5
y
b)
25
−
x
2
−
y
2
−
2
x
y
c)
x
4
+
x
3
+
2
x
2
+...
Đọc tiếp
Phân tích các đa thức sau thành nhân tử
a) x 2 + x y − 5 x − 5 y
b) 25 − x 2 − y 2 − 2 x y
c) x 4 + x 3 + 2 x 2 + x + 1
Tìm đa thức M biết:a)
2
x
6
-
x
4
-
2
x
2
+1 M.(2
x
2
-1);b) (
x
2
+x + 1).M
x
4
-
x
3
- 4
x
2
- 5x - 3.
Đọc tiếp
Tìm đa thức M biết:
a) 2 x 6 - x 4 - 2 x 2 +1 = M.(2 x 2 -1);
b) ( x 2 +x + 1).M = x 4 - x 3 - 4 x 2 - 5x - 3.
a) Kết quả M = x 4 – 1.
b) Kết quả M = x 2 – 2x – 3.
Đúng 0
Bình luận (0)
Cho đa thức: P(x) = x4 - 3x2 + 1/2 - x.
Tìm các đa thức Q(x), R(x) sao cho:
P(x) + Q(x) = x5 - 2x2 + 1
Ta có:
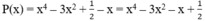
Vì : P(x) + Q(x) = x5 – 2x2 + 1
Suy ra Q(x) = x5 – 2x2 + 1– P(x).
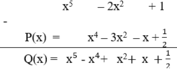
Đúng 0
Bình luận (0)
Bài 2. Cho hai đa thức: P(x) = 5x3 + 3 - 3x2 + x4 - 2x - 2 + 2x2 + x Q(x) = 2x4 + x2 + 2x + 2 - 3x2 - 5x + 2x3 - x4 a) Thu gọn và sắp xếp các hạng tử của mỗi đa thức trên theo lũy thừa giảm dần của biến. b) Tính P(x) + Q(x), P(x) - Q(x), Q(x) - P(x)
ai giúp mình với:(
`@` `\text {Ans}`
`\downarrow`
`a)`
\(P(x) = 5x^3 + 3 - 3x^2 + x^4 - 2x - 2 + 2x^2 + x\)
`= x^4 + 5x^3 + (-3x^2 + 2x^2) + (-2x+x) + (3-2)`
`= x^4 + 5x^3 - x^2 - x + 1`
\(Q(x) = 2x^4 + x^2 + 2x + 2 - 3x^2 - 5x + 2x^3 - x^4\)
`= (2x^4 - x^4) + 2x^3 + (x^2 - 3x^2) + (2x-5x) + 2`
`= x^4 + 2x^3 - 2x^2 - 3x +2`
`b)`
`P(x)+Q(x) = (x^4 + 5x^3 - x^2 - x + 1) + (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 + x^4 + 2x^3 - 2x^2 - 3x +2`
`= (x^4+x^4)+(5x^3 + 2x^3) + (-x^2 - 2x^2) + (-x-3x) + (1+2)`
`= 2x^4 + 7x^3 - 3x^2 - 4x + 3`
`P(x)-Q(x)=(x^4 + 5x^3 - x^2 - x + 1) - (x^4 + 2x^3 - 2x^2 - 3x +2)`
`= x^4 + 5x^3 - x^2 - x + 1 - x^4 - 2x^3 + 2x^2 + 3x -2`
`= (x^4 - x^4) + (5x^3 - 2x^3) + (-x^2+2x^2)+(-x+3x)+(1-2)`
`= 3x^3 + x^2 + 2x - 1`
`Q(x)-P(x) = (x^4 + 2x^3 - 2x^2 - 3x +2)-(x^4 + 5x^3 - x^2 - x + 1)`
`= x^4 + 2x^3 - 2x^2 - 3x +2-x^4 - 5x^3 + x^2 + x - 1`
`= (x^4-x^4)+(2x^3 - 5x^3)+(-2x^2+x^2)+(-3x+x)+(2-1)`
`= -3x^3 - x^2 - 2x + 1`
`@` `\text {Kaizuu lv u.}`
Đúng 3
Bình luận (0)
Tìm tất cả các số thực a sao cho đa thức x4 + x3 -2x2 + x + a chia hết cho đa thức x + 1
Đọc tiếp
Tìm tất cả các số thực a sao cho đa thức x4 + x3 -2x2 + x + a chia hết cho đa thức x + 1
\(x^4+x^3-2x^2+x+a⋮x+1\)
=>\(x^4+x^3-2x^2-2x+3x+3+a-3⋮x+1\)
=>a-3=0
=>a=3
Đúng 0
Bình luận (0)
Bài 1: Phân tích đa thức thành nhân tử
a) x3-2x2-5x+6
b) x4+5x2+6
c) x3+4x2+5x+2
d) x4+324