Cho tam giác cân AOB, có \(\widehat{AOB}\) = 110 độ . Vẽ đường tròn (O; OA). Gọi C là một điểm trên đường tròn (O), biết \(\stackrel\frown{AC}\) = 40độ . Tính số đo của cung nhỏ BC và cung lớn BC .
Những câu hỏi liên quan
Cho tam giác cân AOB có \(\widehat{AOB}\) = 120°. Vẽ đường tròn (O; OA). Gọi M là một điểm nằm trên đường tròn, biết sđ\(\stackrel\frown{AM}\) = 50°. Tính số đo cung nhỏ BM và số đo cung lớn BM.
Cho tam giác cân AOB có góc AOB bằng 110 độ.Vẽ đường tròn tâm O , bán kính OA. Gọi C là một điểm trên đường tròn O , biết số đo cung AC=40 độ.Tính số đo cung nhỏ BC và cung lớn BC.
góc COB=40+110=150 độ
=>sđ cung nhỏ BC=150 độ
sđ cung lớn BC=360-150=210 độ
Đúng 0
Bình luận (0)
Cho tam giác cân AOB có góc AOB bằng 110 độ.Vẽ đường tròn tâm O , bán kính OA. Gọi C là một điểm trên đường tròn O , biết số đo cung AC=40 độ.Tính số đo cung nhỏ BC và cung lớn BC.
Cho em xin lời giải cụ thể với ạ,em cảm ơn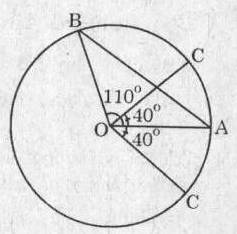
Theo giả thiết: Vì số đo cung \(\stackrel\frown{AC}=40^o\)
\(\Rightarrow\) Góc ở tâm \(\widehat{AOC}=40^o\)
Trường hợp 1: C thuộc cung nhỏ \(\stackrel\frown{AB}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{AOB}-\widehat{AOC}=110^o-40^o=70^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=70^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-70^o=290^o\)
Trường hợp 2: C thuộc cung lớn \(\stackrel\frown{BC}\)
- Số đo góc ở tâm \(\widehat{BOC}=\widehat{BOA}+\widehat{AOC}=110^o+40^o=150^o\)
Do vậy:
- Số đo cung nhỏ \(\stackrel\frown{BC}=150^o\)
- Số đo cung lớn \(\stackrel\frown{BC}=360^o-150^o=210^o\)
Đúng 0
Bình luận (0)
Cho ΔAOB có \(\widehat{AOB}=110^o\) . Vẽ đường tròn (O, OA). Gọi C là 1 điểm trên đường tròn (O) biết sđ \(\stackrel\frown{AC}=40^0\) . Tính số đo cung nhỏ \(\stackrel\frown{BC}\) và cung lớn \(\stackrel\frown{BC}\)
cho đường tròn tâm O và một điểm M nằm ngoài đường tròn . Qua M vẽ các tiếp tuyến MA,MB với đường tròn tâm O . Biết \(\widehat{AMB}\) = 54 độ . Hỏi 2 bán kính OA,OB tạo thành góc ở tâm \(\widehat{AOB}\) bằng bao nhiêu độ
Hình bạn tự vẽ nhé :
Xét tứ giác OAMB có : góc AOB + góc OAM + góc AMB +góc OBM =360 độ
⇒ góc AOB + 90 độ +54 độ +90 độ =360 độ
⇒ góc AOB =360 độ - 90 độ -90 độ -54 độ = 126 độ
Đúng 1
Bình luận (0)
84. Cho tam giác ABC vuông cân tại A. Điểm O ở trong tam giác sao cho \(\widehat{OBC}=30^o;\widehat{OCB}=15^o.\)Chứng minh các tam giác AOC, AOB cân.
vẽ tam giác đều BCM ( M và A cùng thuộc 1 nửa mặt phẳng bờ BC )
CM được tam giác COA cân tại C
\(\widehat{ACO}=45^o-15^o=30^o\)
\(\widehat{CAO}=\left(180^o-30^o\right):2=75^o\)
\(\widehat{BAO}=90^o-75^o=15^o\); \(\widehat{ABO}=45^o-30^o=15^o\)
Vậy \(\widehat{BAO}=\widehat{ABO}\)suy ra : \(\Delta AOB\)cân tại O
Đúng 0
Bình luận (0)
từ điểm M ở ngoài đường tròn (O) vẽ hai tiếp tuyến MA và MB( a,b là tiếp điểm ) . Cho biết góc AMB = 40 độ
a, tính góc AOB
b, từ O kẻ đường thẳng vuông góc với OA cắt MB tại N . cm tam giác OMN là tam giác cân
Cho đường tròn tâm O bán kính R. Vẽ góc ở tâm \(\widehat{AOB}=80^0\), vẽ góc ở tâm \(\widehat{BOC}=120^0\) kề với \(\widehat{AOB}\)
So sánh và sắp xếp độ dài AB, BC, CA theo thứ tự tăng dần ?
Giải mục 1 trang 7 ,8 , 9 SGK Toán 11 tập 1 - Chân trời sáng tạo
16 tháng 7 2023 lúc 16:41
Vẽ đường tròn tâm O bán kính R bất kì. Dùng một đoạn dây mềm đo bán kính và đánh dấu được một cung AB có độ dài đúng bằng R (Hình 9). Đo và cho biết \(\widehat {AOB}\) có số đo bằng bao nhiêu độ.
\( \Rightarrow \widehat {AOB} = 60^\circ \)
Đúng 1
Bình luận (0)