Cho hình thang cân MNPQ. MQ là đáy lớn ; MP cắt NQ tại I. Hai cạnh bên kéo dài cắt nhau tại O. H là trung điểm của MQ. Chứng minh rằng:
a) Tam giác OMQ cân
b) IM=IQ và IN=IP
c) 3 điểm O, I, H thẳng hàng
Cho hình thang MNPQ với đáy lớn là PQ, đáy nhỏ là MN. E là trung điểm MP CMR: các vectơ EM+EN+EP+EQ=PN+MQ
\(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(1)
\(\overrightarrow{PN}+\overrightarrow{MQ}\)
\(=\overrightarrow{PE}+\overrightarrow{EN}+\overrightarrow{ME}+\overrightarrow{EQ}\)
\(=\overrightarrow{EN}+\overrightarrow{EQ}\)(2)
Từ (1) và (2) suy ra \(\overrightarrow{EM}+\overrightarrow{EN}+\overrightarrow{EP}+\overrightarrow{EQ}=\overrightarrow{PN}+\overrightarrow{MQ}\)
Cho hình thang MNPQ có góc P > 90 độ > góc Q và góc N = 2 lần góc M.
a) Xác định các đáy của hình thang MNPQ.
b) Nếu cho thêm MN = NP = MQ:2 = a. C/m MNPQ là hình thang cân. Gọi O là giao điểm của MP & NQ. Tính góc MOQ.
Cho hình thang MNPQ có góc P > 90 độ > góc Q và góc N = 2 lần góc M.
a) Xác định các đáy của hình thang MNPQ.
b) Nếu cho thêm MN = NP = MQ:2 = a. C/m MNPQ là hình thang cân. Gọi O là giao điểm của MP & NQ. Tính góc MOQ.
Cho hình thang MNPQ có góc P > 90 độ > góc Q và góc N = 2 lần góc M.
a) Xác định các đáy của hình thang MNPQ.
b) Nếu cho thêm MN = NP = MQ:2 = a. C/m MNPQ là hình thang cân. Gọi O là giao điểm của MP & NQ. Tính góc MOQ.
Cho hình thang MNPQ có góc P > 90 độ > góc Q và góc N = 2 lần góc M.
a) Xác định các đáy của hình thang MNPQ.
b) Nếu cho thêm MN = NP = MQ:2 = a. C/m MNPQ là hình thang cân. Gọi O là giao điểm của MP & NQ. Tính góc MOQ.
Cho hình thang MNPQ có \(\widehat{P}>90^0>\widehat{Q}\) và \(\widehat{N}=2\widehat{M}\)
a) Xác định đáy của hình thang MNPQ.
b) Nếu thêm MN = NP = MQ/2 = a. CMR: MNPQ là hình thang cân.
cho hình thang MNPQ ( MN là đáy nhỏ) hai đường chéo MP và NQ cắt nhau tại O. Biết NMP=MNQ , qua O vẽ đường thẳng EF // PQ (E thuộc MQ, F thuộc NP) chứng minh NMQP, FEQP , MNFE là hình thang cân
ta có MNPQ là hình thang=>MN//PQ
mà \(=\angle\left(NMP\right)=\angle\left(MNQ\right)=>\angle\left(NQP\right)=\angle\left(MPQ\right)\)
=>tam giác MNO cân tại O=>MO=NO
=>tam giác QOP cân tại O=>OQ=Op
=>MO+OP=NO+OQ=>NQ=MP
=>MNPQ là hình thang cân
\(=>\angle\left(M\right)=\angle\left(N\right)\left(1\right)\)
\(\angle\left(Q\right)=\angle\left(P\right)\left(2\right)\)
mà EF//PQ=>EF//MN
=>MNFE là hình thang(3)
từ (1)(3)=>MNFE là hình thang cân
=>EFPQ là hình thang(4)
(2)(4)=>EFPQ là hình thang cân
Ta có: \(\widehat{OMN}=\widehat{OPQ}\)
\(\widehat{ONM}=\widehat{OQP}\)
mà \(\widehat{OMN}=\widehat{ONM}\)
nên \(\widehat{OPQ}=\widehat{OQP}\)
Xét ΔOMN có \(\widehat{OMN}=\widehat{ONM}\)
nên ΔOMN cân tại O
Xét ΔOPQ có \(\widehat{OPQ}=\widehat{OQP}\)
nên ΔOPQ cân tại O
Ta có: OM+OP=MP
ON+OQ=QN
mà OM=ON
và OP=OQ
nên MP=QN
Hình thang MNPQ có MP=QN
nên MNPQ là hình thang cân
Suy ra: \(\widehat{EMN}=\widehat{FNM}\) và \(\widehat{EQP}=\widehat{FPQ}\)
Hình thang EMNF có \(\widehat{EMN}=\widehat{FNM}\)
nên EMNF là hình thang cân
Hình thang EQPF có \(\widehat{EQP}=\widehat{FPQ}\)
nên EQPF là hình thang cân
cho hình thang cân MNPQ với cạnh đáy MN= 3cm, PQ và NP = 3cm, MP=7cm. tính độ dài MQ, NQ
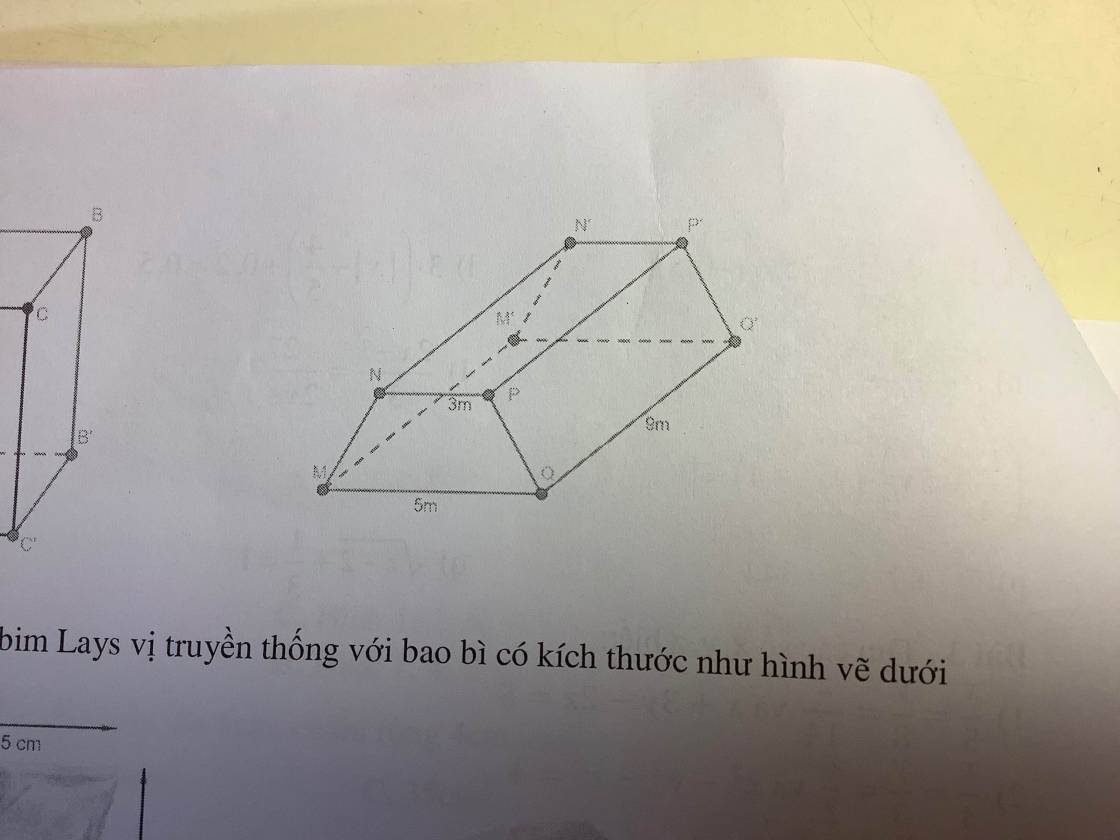
Tính diện tích xung quanh và thể tích hình lăng trụ đứng tam giác MNPQ.M'N'P'Q'. Biết đáy MNPQ là hình thang cân có độ dài 2 cạnh MQ=5m, NP=3m và chiều cao hình thang là 2,83m
cho hình chữ nhật MNPQ gồm hình thang INPQ và hình tam giác MIQ có kích thước QP = 42 cm; NQP = 20 cm. a , Biết đáy bé IN bằng 1/3 đáy lớn PQ. Tính diện tích hình thang INPQ. b, K là trung điểm của cạnh MQ. Tính diện tích hình tam giác IKQ.
Sửa đề; MQ=20cm
a: IN=1/3*42=14cm
S INPQ=1/2(14+42)*20=10*56=560cm2
b: S MIQ=1/2*21*20=210cm2
=>S IKQ=105cm2
Cho hình thang cân MNPQ đáy MN , PQ . Gọi O là giao điểm của MQ và NP.
a, CMR : Tam giác OMN cân .
b, CMR : Tam giác OMP = Tam giác ONQ .
c, Gọi I là giao điểm của MP và NQ .
CMR : Tam giác NIQ = Tam giác MIP .
Vẽ cả hình .!!!