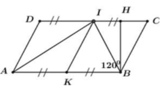
Kẻ BH là đường cao ứng với cạnh CD của hình bình hành ABCD

=> S_ABCD = BH.CD

Theo đề bài ta có chu vi hình bình hành ABCD bằng 60cm.

=> 2(AB + BC) = 60 ó 2.3BC = 60 ó BC = 10cm

Xét tứ giác KICB ta có:

IC = BC = KB = IK = 1 2 AB = 10cm

=> IKBC là hình thoi (dấu hiệu nhận biết).

Mà B ^ = 120⁰ =>  I C B ^  = 180⁰ – 120⁰ = 60⁰

Xét tam giác ICB có: I C = B C I C B = 60 0

=> ICB là tam giác đều. (tam giác cân có góc ở đỉnh bằng 60⁰).

=> BH vừa là đường cao vừa là đường trung tuyến ứng hay H là trung điểm của IC.

=> HI = HC = 1 2 BC = 5cm

Áp dụng định lý Pytago với tam giác vuông HBC ta có:

BH = B C 2 − H C 2 = 10 2 − 5 2 = 75 = 5 3 cm

=> S_ABCD = BH.AB = BH.2BC = 5 3 .2.10 = 100 3 cm²

Đáp án cần chọn là: A

a: Xét tứ giác AMCN có 

AM//CN

AN//CM

Do đó: AMCN là hình bình hành

xét tứ giác AICJ ta có:

AI // CJ (  AB // CD)

AI=CJ ( I VÀ J LÀ TRUNG ĐIỂM CỦA 2 CẠNH AB VÀ CD)

=> TỨ GIÁC AICJ LÀ HÌNH BÌNH HÀNH

 mà trong hình bình hành 2 đg chéo cắt nhau tại trg điểm môic đg 

=> O là trg điểm của IJ

Xét ΔAID và ΔCKB có

AD=CB

góc D=góc B

DI=KB

=>ΔAID=ΔCKB

Xét ΔAIK và ΔCKI có

AI=CK

AK=CI

IK chung

=>ΔAIK=ΔCKI

a/ Xét △AMD vuông tại M và △CNB vuông tại N có:

- \(AD=BC\) (ABCD là hình bình hành)

- \(\hat{ADM}=\hat{CBN}\) (AD // BC)

⇒ △AMD = △CNB (c.h-g.n) ⇒ AM=NC (1)

\(\begin{matrix}AM\perp MN\\AN\perp NC\end{matrix}\left(gt\right)\Rightarrow AM\text{ // }NC\left(2\right)\)

Từ (1) và (2). Vậy: AMCN là hình bình hành (đpcm)

============

b/ AC và MN là hai đường chéo của hình bình hành AMNC

- Mà I là trung điểm MN

Vậy: I là trung điểm của AC (Trong hình bình hành, hai đường chéo cắt nhau tại trung điểm của mỗi đường) (đpcm)

Xét ΔADM vuông tại M và ΔCBN vuông tại N có 

AD=BC

\(\widehat{ADM}=\widehat{CBN}\)

Do đó: ΔADM=ΔCBN

Suy ra: AM=CN

Xét tứ giác AMCN có 

AM//CN

AM=CN

Do đó: AMCN là hình bình hành

Suy ra: Hai đường chéo AC và MN cắt nhau tại trung điểm của mỗi đường

mà I là trung điểm của MN

nên I là trung điểm của AC

a)Vì A đối xứng với F qua N =>N là trung điểm AF

Mà I là trung điểm BF(gt) => NI là đường trung bình của tam giác FAB

=>NI//AB,NI=1/2AB .Mà AB//CD(ABCD là hình chữ nhật) =>NI//CD hay NI//MC(M thuộc CD) (1)

Vì NI=1/2AB(cmt), AB=CD(ABCD là hcn) => NI=1/2CD

Lại có: M là trung điểm CD(gt) => MC=MD=1/2CD =>NI=MC (2)

Từ (1) và (2) => CINM là hình bình hành

b)Vì NI//CD (cmt), CD vuông góc với BC(ABCD là hình bình hành)

=>NI vuông góc với BC =>NI là đường cao trong tam giác NBC (3)

Vì góc BNM=90 độ(gt) =>BN vuông góc với NM

Lại có :NM//IC(CINM là hình bình hành) =>CI vuông góc với BN

=>CI là đường cao trong tam giác BNC (4)

Từ (3) và (4) =>I là trực tâm trong tam giác BNC =>BI vuông góc với AC hay BF vuông góc với AC