Cho tứ giác ABCD có AD=BC. Trên AB,CD lần lượt lấy các điểm M và N là trung điểm của AB và CD; E và F theo thứ tự là giao điểm của AD và BC với đường thẳng MN. Chứng minh rằng: góc AEM = góc BFM

Những câu hỏi liên quan
Cho hình thang ABCD ( AB // CD; AB < CD ). Trên AD lấy AE = EM = MP = PD. Trên BC lấy BF = FN = NQ = QC
a) Chứng minh M, N lần lượt là trung điểm của AD và BC;
b) Tứ giác EFQP là hình gì? Vì sao?
c) Tính MN, EF, PQ biết AB = 8cm và CD = 12cm;
d) Kẻ AH vuông góc CD tại H và AH = 10cm. Tính diện tích tứ giác ABCD.
em cảm ơn ạ!
a: Ta có: AE+EM=MP+PD
nên AM=MD
hay M là trung điểm của AD
Ta có: BF+FN=NQ+QC
nên BN=CN
hay N là trung điểm của BC
Đúng 0
Bình luận (0)
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EFAB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.2. Cho tứ giác ABCD có ADBC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEMgóc MFB.3. Cho tam giác ABC (ABAC). Trên cạnh AB lấy điểm D sao cho BDAC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC 2.BMN4. Cho tứ giác ABCD, gọi A, B, C, D lần lượt là trọng tâm của các tam giác BCD,...
Đọc tiếp
1. Cho tứ giác ABCD ( AD không song song BC) có E,F lần lượt là trung điểm AD, BC và EF=AB+CD/2. Chứng minh rằng tứ giác ABCD là hình thang.
2. Cho tứ giác ABCD có AD=BC. Đường thẳng đi qua trung điểm M và N của 2 cạnh AB và CD cắt AD và BC lần lượt tại E và F. Chứng minh góc AEM=góc MFB.
3. Cho tam giác ABC (AB>AC). Trên cạnh AB lấy điểm D sao cho BD=AC. Gọi M,N lần lượt là trung điểm của AD, BC. Chứng minh góc BAC = 2.BMN
4. Cho tứ giác ABCD, gọi A', B', C', D' lần lượt là trọng tâm của các tam giác BCD, ACD, ABD, ABC. Chứng minh rằng các đường thẳng AA', BB', CC', DD' đồng quy.
5. Cho tam giác ABC, G là trọng tâm. Đường thẳng d không cắt các cạnh của tam giác ABC. Gọi A', B', C', G' lần lượt là hình chiếu của A, B, C, G trên đường thẳng d. Chứng minh GG'=AA'+BB'+CC'/3
bài 1 cho hình thang ABCD (AB // CD và AB CD ) trên đg AD lấy AE EM MP PD .Trên đg BC lấy BF FN NQ QC .1) C/m M, N lần lượt là trung điểm của AD và BC.2) tứ giác EFQP là hình gì ?3) tính MN ,EF ,PQ biết AB 8 cm và CD 12 cm4) kẻ AH vuông góc tại H và AH 10 cm . tính S_{ABCD}bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD DE EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại M, N . C/m rằng : 1) M là trung điểm của AN.2) AM MN NC .3) 2EN DM + BC .4)S_{ABC}3S_{...
Đọc tiếp
bài 1 cho hình thang ABCD (AB // CD và AB < CD ) trên đg AD lấy AE = EM = MP = PD .Trên đg BC lấy BF = FN = NQ = QC .
1) C/m M, N lần lượt là trung điểm của AD và BC.
2) tứ giác EFQP là hình gì ?
3) tính MN ,EF ,PQ biết AB = 8 cm và CD = 12 cm
4) kẻ AH vuông góc tại H và AH = 10 cm . tính \(S_{ABCD}\)
bài 2 cho tam giác ABCD . Trên cạnh AB lấy AD = DE = EB . Từ D, E kẻ các đg thẳng cùng song song với BC cắt cạnh AC lần lượt tại M, N . C/m rằng : 1) M là trung điểm của AN.
2) AM = MN = NC .
3) 2EN = DM + BC .
4)\(S_{ABC}=3S_{AMB}\)
bài 3 : cho hình thang ABCD ( AB //CD ) có đg cao AH = 3 cm và AB = 5cm , CD = 8cm gọi E, F , I lần lượt là trung điểm của AD , BC và AC.
1) C/m E ,F ,I thẳng hàng .
2) tính \(S_{ABCD}\)
3) so sánh \(S_{ADC}\) và \(2S_{ABC}\)
bài 4: cho tứ giác ABCD . gọi E, F, I lần lượt là trung điểm AD , BC và AC .1) C/m E, I , F thẳng hàng
2) tính EF≤ AB+CD / 2
3) tứ giác ABCD phải có điều kiện gì thì EF = AB+CD / 2
Cho tứ giác ABCD có M, N, P, Q lần lượt là trung điểm của AB, BC, CD và AD. Trên AB lấy điểm E không trùng với điểm M, trên DC lấy điểm F. Biết tứ giác ENFQ là hình bình hành. CMR:
a) Tứ giác MNPQ là hình bình hành
b) AB//CD
c) SENFQ = 1/2 SABCD
Cho tứ giác ABCD có AD=BC và AB<CD. Trung điểm của cạnh AB và CD lần lượt là
M và N. Trung điểm của các đường chéo BD và AC lần lượt là P và Q.
a) Chứng minh tứ giác MPNQ là hình thoi
b) Kéo dài hai cạnh DA và CB cắt nhau tại G, kẻ tia phân giác Gx của góc AGB. Chứng
minh Gx//MN.
Cho hình thang ABCD có AB// CD; AB 10cm , CD 12cm, đường cao AH 6cm . Gọi M và N lần lượt là trung điểm của AD và BC. Tính diện tích tứ giác ABNM? A. 30
c
m
2
B. 29,5
c
m
2
C. 27,5
c
m
2
D.31,5
c
m
2
Đọc tiếp
Cho hình thang ABCD có AB// CD; AB = 10cm , CD = 12cm, đường cao AH = 6cm . Gọi M và N lần lượt là trung điểm của AD và BC. Tính diện tích tứ giác ABNM?
A. 30 c m 2
B. 29,5 c m 2
C. 27,5 c m 2
D.31,5 c m 2
Xét hình thang ABCD có M và N lần lượt là trung điểm của AD và BC nên MN là đường trung bình của hình thang:
Suy ra: MN// AB// CD và
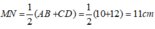
Suy ra: tứ giác MNCD là hình thang.
Vì M là trung điểm của AD và đường cao AH = 6cm nên chiều cao xuất phát từA của hình thang MNCD là:
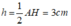
Diện tích hình thang ABNM là :
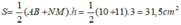
Chọn đáp án D
Đúng 0
Bình luận (0)
Cho hình thang ABCD (AB // CD). Trên AB, CD lần lượt lấy thêm 3 điểm và 5 điểm. Có thể nối tạo bao nhiêu tam giác từ các điểm trên hình biết tam giác có 1 diểm trên CD, 1 điểm trên AB và trung điểm M của AD
Số tam giác tạo được là 3*5=15(tam giác)
Đúng 0
Bình luận (0)
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho
P
A
→
m
P
D
→
và
Q
B
→
m
Q
C
→
, với m khác 1. Vecto
M
P...
Đọc tiếp
Cho tứ diện ABCD. Các điểm M và N lần lượt là trung điểm của AB và CD. Lấy hai điểm P và Q lần lượt thuộc AD và BC sao cho P A → = m P D → và Q B → = m Q C → , với m khác 1. Vecto M P → bằng:
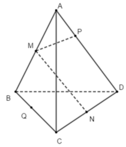
A. M B → − m Q C →
B. M N → − m P D →
C. M A → − m P D →
D. M N → − m Q C →
Có thể loại các phương án A, B và D vì các cặp ba vecto ( M P → , M B → , v à Q C → ) , ( M P → , M N → , P D → ) và ( M P → , M N → v à Q C → ) đều không đồng phẳng.
Phương án C đúng vì : M P → = M A → + A P → = M A → - m P D →
Đáp án C
Đúng 0
Bình luận (0)
cho tứ giác ABCD . gọi M,N lần lượt là trung điểm AB và CD .cmr: a) 2overrightarrow{mn}overrightarrow{AC}+overrightarrow{BD}overrightarrow{BC}+overrightarrow{AD}b)Lấy H trên AD , K trên BC sao cho dfrac{HA}{HD}dfrac{KB}{KC}. HK cắt MN tại I .cmr I là trung điểm HK
Đọc tiếp
cho tứ giác ABCD . gọi M,N lần lượt là trung điểm AB và CD .cmr:
a) 2\(\overrightarrow{mn}\)=\(\overrightarrow{AC}\)+\(\overrightarrow{BD}\)=\(\overrightarrow{BC}\)+\(\overrightarrow{AD}\)
b)Lấy H trên AD , K trên BC sao cho \(\dfrac{HA}{HD}\)=\(\dfrac{KB}{KC}\). HK cắt MN tại I .cmr I là trung điểm HK












