Cho tam giác ABC vuông tại A. Tia phân giác của góc B cắt AC ở D; E là 1 điểm nằm trên cạnh BC sao cho BE = BA.
a) CM: DE vuông góc với BC
b) Gọi F là giao điểm của DE và AB. CMR DE = DF
c) CM: AD<DC
d) CM BD là đường trung trực của AE và AE // FC
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A. Gọi (d) là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt (d) ở E, biết. Tính các góc của tam giác CDE. 
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. CMR tam giác CDE có 2 góc bằng nhau
Bạn xem ở đây nhé:
Câu hỏi của Ngọc Đậu Nguyễn Yến - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có hai góc bằng nhau.
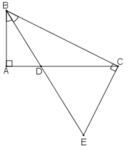
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)
+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)
+) Tam giác ABD vuông tại A nên:
∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)
Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)
+) Tam giác BCE vuông tại C nên:
∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)
Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)
Vậy tam giác CDE có hai góc bằng nhau.
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A có AB < AC.
a, So sánh các góc của tam giác ABC.
b, tia phân giác của góc ABC và tia phân giác của góc ACB cắt nhau tại I. So sánh IB và IC.
c, gọi d là đường thẳng vuông góc với BC tại C. tia BI kéo dài cắt AC ở D và cắt đường thẳng d tại M. chứng minh CDM = CMD
a:
ΔABC vuông tại A nên BC là cạnh lớn nhất
=>AC<BC
mà AB<AC
nên AB<AC<BC
Xét ΔABC có AB<AC<BC
mà \(\widehat{C};\widehat{B};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: Ta có: \(\widehat{ABI}=\widehat{CBI}=\dfrac{\widehat{ABC}}{2}\)
\(\widehat{ACI}=\widehat{BCI}=\dfrac{\widehat{ACB}}{2}\)
mà \(\widehat{ACB}< \widehat{ACB}\)
nên \(\widehat{ICB}< \widehat{IBC}\)
Xét ΔIBC có \(\widehat{ICB}< \widehat{IBC}\)
mà IB,IC lần lượt là cạnh đối diện của các góc ICB và góc IBC
nên IB<IC
Đúng 1
Bình luận (1)
Cho tam giác ABC vuông tại A (AB>AC). Tia phân giác của góc B cắt AC ở D. Kẻ DH vuông góc với BC. Trên tia AC lấy E sao cho AE=AB. Đường thẳng vuông góc AE tại E cắt tia BH tại K
Chọn câu đúng
A. BH = BD
B. BH > BA
C. BH < BA
D. BH = BA
Cho tam giác ABC vuông tại A (AB>AC). Tia phân giác của góc B cắt AC ở D. Kẻ DH vuông góc với BC. Trên tia AC lấy E sao cho AE=AB. Đường thẳng vuông góc AE tại E cắt tia BH tại K
Tính số đo góc DBK
A. 45 °
B. 30 °
C. 60 °
D. 40 °
cho tam giác abc vuông tại a ( ac>ab ), tia phân giác của góc a cắt bc ở d. Đường thẳng vuông góc với bc tại d cắt ac ở e. chứng minh DB= DE
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có hai góc bằng nhau
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có 2 góc bằng nhau
Bạn xem ở đây nhé:
Câu hỏi của Ngọc Đậu Nguyễn Yến - Toán lớp 7 - Học toán với OnlineMath
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có hai góc bằng nhau ?
(hình hơi xấu ạ :V)
\(\widehat{D_2}=\widehat{D_1}\), \(\widehat{D_1}\) phụ với \(\widehat{B_1}\) nên:
\(\widehat{D_2}\) phụ với \(\widehat{B_1}\) (1)
\(\widehat{E_1}\) phụ với \(\widehat{B_2}\) (2)
\(\widehat{B_1}=\widehat{B_2}\) (3)
Từ (1), (2), (3) => \(\widehat{D_2}=\widehat{E_1}\)
Đúng 0
Bình luận (0)