Question

Cho tam giác ABC vuông tại A. Gọi d là đường thẳng vuông góc với BC tại C. Tia phân giác của góc B cắt AC ở D và cắt d ở E. Chứng minh rằng tam giác CDE có hai góc bằng nhau.

Answer 1

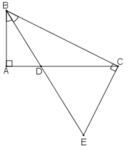
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)

+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)

+) Tam giác ABD vuông tại A nên:

∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)

Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)

+) Tam giác BCE vuông tại C nên:

∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)

Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)

Vậy tam giác CDE có hai góc bằng nhau.