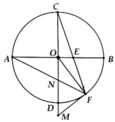
Cho (O) đường kính AB. Trên AB lấy một điểm E. Qua E vẽ dây CD vuông góc với AB. Vẽ các dây DN; CM đi qua F. Chứng minh rằng NI = IM

Những câu hỏi liên quan
cho (O,AB/2), E thuộc AB.Qua E vẽ dây CD vuông góc với AB. Trên BE lấy F vẽ các dây CM,DN đi qua F. chứng minh CMND cân
Cho đường tròn (O) đường kính AB. Trên các bán kính OA và OB lấy các điểm M và N sao cho OM ON. Qua M và N lần lượt vẽ các dây CD và EF song song với nhau (C và E nằm cùng phía với AB). Từ O kẻ một đường thẳng vuông góc với 2 dây song song vừa vẽ, đường thẳng này cắt CD tại I và cắt FE tại J. Chứng minh: a) Tam giác OIM bằng tam giác OJN b) Hai dây CD và EF bằng nhau c) Tứ giác IJEC là hình chữ nhật d) Tứ giác CDFE là hình chữ nhật
Đọc tiếp
Cho đường tròn (O) đường kính AB. Trên các bán kính OA và OB lấy các điểm M và N sao cho OM = ON. Qua M và N lần lượt vẽ các dây CD và EF song song với nhau (C và E nằm cùng phía với AB). Từ O kẻ một đường thẳng vuông góc với 2 dây song song vừa vẽ, đường thẳng này cắt CD tại I và cắt FE tại J. Chứng minh: a) Tam giác OIM bằng tam giác OJN b) Hai dây CD và EF bằng nhau c) Tứ giác IJEC là hình chữ nhật d) Tứ giác CDFE là hình chữ nhật
Cho đường tròn tâm o đường kính AB,E thuộc AB.Qua E vẽ dây CD vuông góc với AB.Trên đoạn BE lấy diểm F vẽ dây CM và DN đi qua F.Chứng minh rằng tứ giác CDMN là hinh thang cân
em ko bt em mới học lớp 8 à tk cho em ik
Đúng 0
Bình luận (0)
tứ giác CNMD nội tiếp đg tròn tâm 0.suy ra gốc MDF= MCN.
tam giác CNF và MFD có:
góc CFN=DFM
CF=FD
gốc MDF= MCN
=> NFC=MFD(g c g)
=> CN=FN, FN=FM (1)
gọi I là giao điểm của NM và AB
tam giác NFI=MFI=>AB vuông góc với NM mà AB vg vs CD
=> CDNM là hình thang (2)
Từ (1)(2)=> đpcm
~HỌC TỐ ~
Đúng 0
Bình luận (0)
Cho đường tròn (O;3cm). Vẽ đường kính AB, lấy điểm M trên AB sao cho AM = 2cm. Qua M vẽ dây CD vuông góc với AB.
a) Tính độ dài đoạn AC
b) Gọi E là điểm đối xứng với A qua điểm M. Tứ giác ACED là hình gì? Vì sao?
c) Vẽ đường tròn tâm O' đường kính EB cắt BC tại K. Tính EK và chứng minh ba điểm D, E, K thẳng hàng
d) Chứng minh MK là tiếp tuyến của đường tròn O'
Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE=R. căn2 . Vẽ dây CF đi qua E . Tiếp tuyến của đường tròn tại F cắt CD tại M , vẽ dây AF cắt CD tại N. CMR: a) MF // AC b) MN, OD, OM là độ dài 3 cạnh của một tam giác
cho đường tròn tâm O và 1 dây AB , vẽ đường kính CD vuông góc AB (D thuộc AnB^ trên cung nhỏ BC^ lấy điểm N . Các đường thẳng CN, DN cắt cạnh AB tại E, F . Trung tuyến của đường tròn tâm O tại N cắt cạnh AB tại I . Cm: IN=IF=IE
Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE R
2
. Vẽ dây CF đi qua E. Tiếp tuyên của đường tròn tại F cắt CD tại M, vẽ dây Aỉ cắt CD tại N. Chứng minh:a, Tia CF là tia phân giác của góc BCDb, MF và AC song songc, MN, OD, OM là độ dài 3 cạnh của một tam giác vuông
Đọc tiếp
Cho (O) có hai đường kính AB và CD vuông góc với nhau. Trên đường kính AB lấy điểm E sao cho AE = R 2 . Vẽ dây CF đi qua E. Tiếp tuyên của đường tròn tại F cắt CD tại M, vẽ dây Aỉ cắt CD tại N. Chứng minh:
a, Tia CF là tia phân giác của góc BCD
b, MF và AC song song
c, MN, OD, OM là độ dài 3 cạnh của một tam giác vuông
a, Học sinh tự chứng minh
b, Chứng minh: A F M ^ = C A F ^ ( = A C F ^ ) => MF//AC
c, Chứng minh: M F N ^ = M N F ^ => ∆MNF cân tại M => MN = MF
Mặt khác: OD = OF = R
Ta có MF là tiếp tuyến nên DOFM vuông => ĐPCM
Đúng 0
Bình luận (0)
Cho đường tròn (O; 2,5) đường kính AB. Trên AB lấy điểm H sao cho AH1. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm đối xứng với A qua H.a)Chứng minh tứ giác ACED là hình thoib)Gọi I là giao điểm của DE và BC. Vẽ đường tròn (O) đường kính EB. Chứng minh rằng đường tròn này đi qua I.c)Chứng minh rằng HI là tiếp tuyến của đường tròn (O)d)Tính độ dài HI
Đọc tiếp
Cho đường tròn (O; 2,5) đường kính AB. Trên AB lấy điểm H sao cho AH=1. Vẽ dây CD vuông góc với AB tại H. Gọi E là điểm đối xứng với A qua H.
a)Chứng minh tứ giác ACED là hình thoi
b)Gọi I là giao điểm của DE và BC. Vẽ đường tròn (O') đường kính EB. Chứng minh rằng đường tròn này đi qua I.
c)Chứng minh rằng HI là tiếp tuyến của đường tròn (O')
d)Tính độ dài HI

cho đường tròn O đường kính AB=8cm trên tia OB lấy I sao cho OI=1cm vẽ dây CD vuông góc AB tại I E là điểm đối xứng của A qua I tính đoạn thẳng CD
ΔOCD cân tại O có OI là đường cao
nên I là trung điểm của CD
CI=căn OC^2-OI^2=căn 4^2-1^2=căn 15(cm)
=>CD=2*căn 15(cm)
Đúng 0
Bình luận (0)














