Cho hình thang ABCD vuông tại A và D . Biết AB=18 ; CD=32 , hai đường chéo AC và BD vuông góc với nhau . Tính AC, AD

Những câu hỏi liên quan
cho hình thang ABCD vuông tại A và D, hai đường cháo AC và BD vuông góc với nhau. Biết AB=18 và CD=32. khi đó AD=
chỉ cần chứng minh tam giác ABD đồng dạng tam giác DAC
==>\(\frac{AD}{DC}=\frac{AB}{AD}\)
==>\(AD^2=AB\cdot DC\)
LẮP VÀO TÍNH LÀ XONG
Đúng 0
Bình luận (0)
Dân ta phải biết sử ta cái gì không biết thì tra google
Ai đồng ý thì tick mình cái
Đúng 0
Bình luận (0)
AC x BD tại O
COD đồng dạng ABO với k=32/18 =16/9
Gọi OA = x ; OB = y => OC = 16/9 x ; OD = 16/9 y
Pitago OAB => x2 +y2 = 182 (1)
Hệ thức lương ADC vuông tại D ( h2 = b'.c')
\(\left(\frac{16}{9}y\right)^2=x.\frac{16}{9}.x\Leftrightarrow x^2=\frac{16}{9}y^2\)(2)
(1)(2) => \(\frac{25}{9}y^2=18^2\Leftrightarrow y=\frac{18.3}{5}=\frac{54}{5}\)
\(\Leftrightarrow x^2=\frac{16}{9}.\frac{54^2}{25}=\left(\frac{4.54}{3.5}\right)^2\Leftrightarrow x=\frac{72}{5}\)
\(\left(\frac{16}{9}y\right)^2=\frac{16}{9}.x^2\)
Pita go AOD => AD2 = x2 + \(\left(\frac{16}{9}y\right)^2\)= x2 + \(\frac{16}{9}.x^2\)=\(\frac{25}{9}.x^2\)
=>AD = \(\frac{5}{3}x=\frac{5}{3}.\frac{72}{5}=24\)
Đúng 0
Bình luận (0)
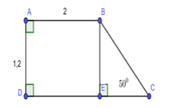
Cho hình thang ABCD vuông tại A và D;
C
^
50
0
. Biết AB 2; AD 1,2. Tính diện tích hình thang ABCD A.
S
A
B
C
D
2 (đvdt) B.
S
A
B
C
D
3 (đvdt) C. ...
Đọc tiếp
Cho hình thang ABCD vuông tại A và D; C ^ = 50 0 . Biết AB = 2; AD = 1,2. Tính diện tích hình thang ABCD
A. S A B C D = 2 (đvdt)
B. S A B C D = 3 (đvdt)
C. S A B C D = 4 (đvdt)
D. S A B C D = 5 2 (đvdt)
Cho hình thang ABCD vuông góc tại A và D . Hai đường chéo vuông góc với nhau tại O. Biết AB =2√13 , OA =6 . Tính diện tích hình thang ABCD
* Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB=\(2\sqrt{13}\), OA=6, tính diện tích hình thang ABCD
Xét tam giác vuông OAB:
\(OB=\sqrt{AB^2-OA^2}=4\)
Áp dụng hệ thức lượng cho tam giác vuông ABD với đường cao AO:
\(AB^2=OB.BD\Rightarrow BD=\dfrac{AB^2}{OB}=13\)
\(\Rightarrow\left\{{}\begin{matrix}OD=BD-OB=9\\AD=\sqrt{BD^2-AB^2}=\sqrt{29}\end{matrix}\right.\)
\(\widehat{BAO}=\widehat{DCO}\left(slt\right)\Rightarrow\Delta_VAOB\sim\Delta_VCOD\) (g.g)
\(\Rightarrow\dfrac{AB}{DC}=\dfrac{OB}{OD}\Rightarrow DC=\dfrac{AB.OD}{OB}=\dfrac{9\sqrt{13}}{2}\)
\(S_{ABCD}=\dfrac{1}{2}AD.\left(AB+CD\right)=\dfrac{1}{2}.\sqrt{29}.\left(2\sqrt{13}+\dfrac{9\sqrt{13}}{2}\right)=...\)
Đúng 1
Bình luận (0)
cho hình thang ABCD vuông tại A và D. AC vuông góc với BD tại O. cho biết AB=18 cm, CD=32 cm. chứng minh các dộ dài AC, BD, AB=CD là độ dài của 3 cạnh 1 tam giác vuông
Cho hình thang abcd vuông tại a và d cho biết ab=12cm cd=18cm,ad=8cm.Tính diện tích hình thang abcd, tỉ số phần trăm diện tích tam giác bcd và diện tích hình thang abcd
ABCD là hình thang vuông tại A và D
=>\(S_{ABCD}=\dfrac{1}{2}\cdot AD\cdot\left(BA+CD\right)=\dfrac{1}{2}\cdot8\cdot\left(12+18\right)=4\cdot30=120\left(cm^2\right)\)
Diện tích tam giác ABD là:
\(S_{ABD}=\dfrac{1}{2}\cdot AB\cdot AD=\dfrac{1}{2}\cdot12\cdot8=4\cdot12=48\left(cm^2\right)\)
Ta có: \(S_{ABD}+S_{BDC}=S_{ABCD}\)
=>\(S_{BDC}+48=120\)
=>\(S_{BDC}=72\left(cm^2\right)\)
=>\(\dfrac{S_{BCD}}{S_{ABCD}}=\dfrac{72}{120}=\dfrac{3}{5}=60\%\)
Đúng 1
Bình luận (0)
Cho hình thang ABCD vuông góc tại A và D. Hai đường chéo vuông góc với nhau tại O. Biết AB= 2 căn 13, OA=6. Tính diện tích hình thang ABCD.
cho hình thang vuông tại A và D, 2 đường chéo AC và DB cắt nhau và vuông góc tại O, biết AB=2√13, OA=6. Tính diện tích hình thang ABCD
cho hình thang vuông abcd vuông tại a và d . biết đáy bé ab=ad=25cm.
a,tìm diện tích hingf thang vuông abcd biết ab=1/4 cd
. b, ac và bd cắt nhau tại e . tìm diện tích hình tam giác dec
mình đang cần gấp