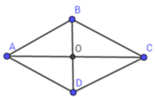
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:

BO = A B 2 − O A 2 = 20 2 − 16 2 = 12

S_ABCD = 1 2 BD. AC =  1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm²)

Đáp án cần chọn là: A

Lời giải:

Độ dài đường chéo BD của hình thoi:

$20\times 2:10=4$ (cm)

Giải:

độ dài đường chéo BD là:

20×2÷10=4(cm)

Độ dài đường chéo BD là : 

    \(20\times\dfrac{3}{5}=12\left(cm\right)\)

Diện tích hình thoi ABCD là : 

   \(\dfrac{20\times12}{2}=120\left(cm^2\right)\)

               Đ/S : \(120cm^2\)

tặng COIN thì mới trả lời

giải

Đường chéo BD là:

   20x2/5=8(cm)

Diện tích hình thoi là:

   20x8:2=80(\(cm^2\))

        Đ/S:80 \(cm^2\)

3/3/4=17/4

Độ dài đường chéo BD là :

17/4-11/20=29/20(dm)

Diện tích hình thoi là :

(17/4x29/20):2=493/560(dm2)

Đ/S:493/560(dm2)

đúng ko mn

Đáp án B

Vì tứ giác ABCD là hình thoi có 2 đường chéo AC= BD nên tứ giác ABCD là hình vuông ( dấu hiệu nhận biết hình vuông)..

Gọi O là tâm hình vuông.

Theo tính chất hình vuông ta có:

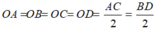
Do đó, O là tâm đường tròn ngoại tiếp hình vuông ABCD.

Gọi \(O\) là giao điểm của \(AC\)và \(BD\).

Theo đề ta có: \(\hept{\begin{cases}AC=8cm\\BD=6cm\end{cases}}\)

Theo tính chất của hình thoi ta có: \(\hept{\begin{cases}AO=OC=4cm\\BO=OD=3cm\end{cases}}\)

Áp dụng định lí Pitago trong \(\Delta AOB\) có:

\(AB^2=AO^2+OB^2\)

\(\Rightarrow AB=\sqrt{AO^2+OB^2}=\sqrt{4^2+6^2}\)

\(\Rightarrow AB=5cm\)

\(\Rightarrow S_{ABCD}=4AB=4.5=20cm\)

Vậy ...............

B

B

B

Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)

\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)

\(\Rightarrow8a^2=32\)

\(\Rightarrow a^2=4\)

\(\Rightarrow a=2\left(cm\right)\)