Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Biết AB = 10cm; AM = 8cm. Tính BM và BC.
Giúp mk các bạn ơi !
Cho tam giác ABC có AB = AC. Gọi M là trung điểm của BC. Biết AB = 10cm; AM = 8cm. Tính BC
Xét ΔABM vuông tại M có
\(AB^2=BM^2+AM^2\)
=>BM=6(cm)
=>BC=12(cm)
Vì tam giác ABC cân nên AM là đường trung tuyến đồng thời là đường cao Theo định lí Pytago cho tam giác AMB vuông tại M
BM = \(\sqrt{AB^2-AM^2}=6\)cm
=> BC = 2BM = 12 cm
ta có: AB=AC => tam giác ABC cân tại A
M là trung điểm BC=> M là đường cao của tam giác ABC
xét tam giác AMB có, M vuông
áp dụng định lý pitago ta có:
\(AB^2=AM^2+MB^2\)
\(10^2=8^2+MB^2\)
=> MB= 6 cm
Mà M là trung điểm BC
=> BC=MB.2=6.2=12cm
cho tam giác ABC gọi M,N,P lần lượt là trung điểm của AB ,AC, BC tính chu vi tam giác mnp biết AC =10cm ,BC =10cm
Cho tam giác ABC, gọi M,N,P theo thứ tự là trung điểm của AB, BC, CA. Tính cu vi của tam giác MNP biết AB =8cm , BC=12cm, AC=10cm
Cho tam giác ABC vuông tại A có AB = 6cm; BC = 10cm; AC = 8cm
a. So sánh các góc của tam giác ABC
b. Trên tia đối tia AB lấy điểm D sao cho A là trung điểm của đoạn thẳng BD. Gọi K là trung điểm của cạnh BC, đường thẳng DK cắt cạnh AC tại M. Tính MC
c. Đường trung trực d của đoạn thẳng AC cắt đường thẳng DC tại Q. Chứng minh ba điểm B, M, Q thẳng hàng
a: Xét ΔABC có AB<AC<BC
nên góc C<góc B<góc A
b: Xét ΔCDB có
CA,DK là trung tuyến
CA cắt DK tại M
=>M là trọng tâm
=>CM=2/3CA=16/3(cm)
c: Gọi giao của d với AC là N
d là trung trực của AC
=>d vuông góc AC tại N và N là trung điểm của AC
=>QN//AD
Xét ΔCAD có
N là trung điểm của AC
NQ//AD
=>Q là trung điểm của CD
Xét ΔCDB có
BQ là trung tuyến
M là trọng tâm
=>B,M,Q thẳng hàng
a, Ta có: AB < AC < BC
=> C < B< A
b, Xét tam giác BCD có CA và DK là đường trung tuyến
CA cắt DK tại M
=> M là trọng tâm tam giác BCD
=> MC= 2/3 AC= 2/3.8= 16/3 cm
c, Xét tam giác ABC và tam giác ADC có:
AB = AD
BAC= DAC= 90°AC chung
=> tam giác ABC = tam giác ADC (c.g.c)
=> ACB= ACD (2 góc tương ứng) và BC = DC ( 2 cạnh tương ứng) (1)
KQ là đường trung trực của AC
=> KQ vuông góc với AC tại E
Xét tam giác KCE và tam giác QCE có:
KCE= QCE
EC chung
KEC= QEC=90°
=> tam giác KCE = tam giác QCE (gcg)
=> KC = QC (2 cạnh tương ứng) (2)
Mà K là trung điểm BC (3)
Từ (1), (2) và (3) suy ra Q là trung điểm của DC
Xét tam giác BCD có M là trong tâm
=> M thuộc đường trung tuyến BQ
=> B, M, Q thẳng hàng
Cho tam giác abc có ab=6cm,ac=8cm,bc=10cm a)Chứng minh tam giác abc vuông tại a b)Gọi M là trung điểm của ac,trên tia đối của tia mb lấy điểm d sao cho mb=md.Chứng minh ab//cd
a) Xét tam giác ABC có:
BC2 = 102 = 100 (cm)
AB2 + AC2 = 62 + 82 = 36 + 64 = 100 (cm)
=> BC2 = AB2 + AC2 (= 100)
=> Tam giác ABC vuông tại A (định lý Pytago đảo)
b) MB = MD (gt) => M là trung điểm BD
Xét Tứ giác ABCD có:
M là trung điểm của BD (cmt)
M là trung điểm của AC (gt)
=> ABCD là hình bình hành (dhnb)
=> AB // CD (Tính chất hình bình hành)
1) Cho tam giác ABC cân tại A có AH là đường cao
a) Biết AB=8cm, BC=4cm. Tính diện tích tam giác ABC
b) Gọi N là trung điểm của AC. Tứ giác ANHB là hình gì?
2) Cho tam giác ABC cân tại A
a) Biết AB=10cm, BC=5cm. Đường trung tuyến AH. Tính diện tích tam giác ABC
b) Gọi M, N lần lượt là trung điểm của AB,AC. Tứ giác BMNC là hình gì?
Mn giúp mik vs bài này mik cần gấp!
Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
\(\Leftrightarrow AH=\dfrac{5\sqrt{15}}{2}\left(cm\right)\)
\(S=\dfrac{\dfrac{5\sqrt{15}}{2}\cdot5}{2}=\dfrac{25\sqrt{15}}{4}\left(cm^2\right)\)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà \(\widehat{B}=\widehat{C}\)
nên BMNC là hình thang cân
Cho tam giác ABC có AB = 6cm, AC = 8cm và BC = 10cm. Gọi M là trung điểm của BC. Từ M kẻ đường thẳng vuông góc với AB cắt AB tại N. Tính MN?
A. 4cm
B. 5cm
C. 6cm
D. 3cm
* Ta có: A B 2 + A C 2 = B C 2 ( 6 2 + 8 2 = 10 2 = 100 )
Suy ra: tam giác ABC vuông tại A
⇒ AB ⊥ AC
* Lại có: MN ⊥ AB nên MN // AC.
* Vì MN // AC và M là trung điểm của BC nên N là trung điểm của AB.
Khi đó, MN là đường trung bình của tam giác ABC .
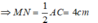
Chọn đáp án A
Cho tam giác ABC có AB = 6cm; BC = 10cm; AC = 8cm. Gọi M là trung điểm của BC. Trên tia đối của tia MA lấy điểm E sao cho ME = MA. Trên tia đối của tia AB lấy điểm D sao cho AD = AB.
a. Tam giác ABC là tam giác gì? Vì sao?
b. Chứng minh AB = EC và AB // CE.
c. Chứng minh tam giác BCD là tam giác cân.
d. Đường thẳng đi qua M và vuông góc với BC cắt AC tại O. Chứng minh rằng điểm O cách đều ba đỉnh của tam giác BDC.
a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét tứ giác ABEC có
M là trung điểm của BC
M là trung điểm của AE
Do đó: ABEC là hình bình hành
Suy ra: AB//EC và AB=EC
c: Xét ΔBCD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔBCD cân tại C
d: Xét ΔOBC có
OM là đường cao
OM là đường trung tuyến
Do đó: ΔOBC cân tại O
Suy ra: OB=OC(1)
Xét ΔOBD có
OA là đường cao
OA là đường trung tuyến
Do đó: ΔOBD cân tại O
Suy ra: OB=OD(2)
Từ (1) và (2) suy ra OB=OC=OD
hay O cách đều ba đỉnh của ΔBDC
Cho tam giác nhọn ABC (AB<AC). Gọi D là trung điểm AB
E là trung điểm AC
M là trung điểm BC
a) Cho DE= 10cm tính BC=?
b) tứ giác BDEC là gì? tại sao?
c) Chứng minh tứ giác BDEM là hình bình hành
a: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔABC
Suy ra: \(DE=\dfrac{BC}{2}\)
hay BC=20(cm)