3:

góc C=90-50=40 độ

Xét ΔABC vuông tại A có sin C=AB/BC

=>4/BC=sin40

=>\(BC\simeq6,22\left(cm\right)\)

\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)

1:

góc C=90-60=30 độ

Xét ΔABC vuông tại A có

sin B=AC/BC

=>3/BC=sin60

=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)

=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)

Áp dụng định lý Py-ta-go đối với ▲MPQ vuông tại M ta có:

\(MQ^2=PQ^2-MP^2\)

\(\Rightarrow MQ=10^2-6^2=100-36=64\)

\(\Rightarrow MQ=8\left(cm\right)\)

Xét ▲ABC và ▲MPQ ta có :

\(\frac{AB}{MP}=\frac{AC}{MQ}=\frac{1}{2}\left(\frac{3}{6}=\frac{4}{8}\right)\)

<A=<M=90

Do đó hai tam giác đồng dạng

- Đâu cần phiền phức vậy! Có hai góc A và M cùng =90 độ lập tỉ số 2 cặp cạnh đã cho độ dài => 2 tỉ số bằng nhau => Tam giác đồng dạng trường hợp c.g.c .

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc B chung

=>ΔHBA đồng dạng với ΔABC

b: \(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)

AH=3*4/5=2,4cm

a. Xét ΔHBA và ΔABC có:

       \(\widehat{H}=\widehat{A}\) = 90⁰ (gt)

        \(\widehat{B}\) chung

\(\Rightarrow\)  ΔHBA \(\sim\) ΔABC (g.g)

b. Vì  ΔABC vuông tại A

Theo đ/lí Py - ta - go ta có:

  BC² = AB² + AC²

  BC² = 3² + 4²

\(\Rightarrow\) BC² = 25 cm

\(\Rightarrow\) BC = \(\sqrt{25}=5\) cm

Ta lại có:  ΔHBA \(\sim\) ΔABC

   \(\dfrac{AH}{CA}=\dfrac{BA}{BC}\) 

\(\Leftrightarrow\dfrac{AH}{4}=\dfrac{3}{5}\) 

\(\Rightarrow\) AH = 2,4 cm

a) Xét ΔABC có \(BC^2=AB^2+AC^2\)

nên ΔABC vuông tại A

Xét Δ BAD và Δ BED

Ta có : BD là cạnh chung

            \(\widehat{BAD}=\widehat{BED}=90^o\)

            \(\widehat{ABD}=\widehat{EBD}\) (BD là tia phân giác \(\widehat{ABC}\))

=> Δ BAD = Δ BED (g.c.g)

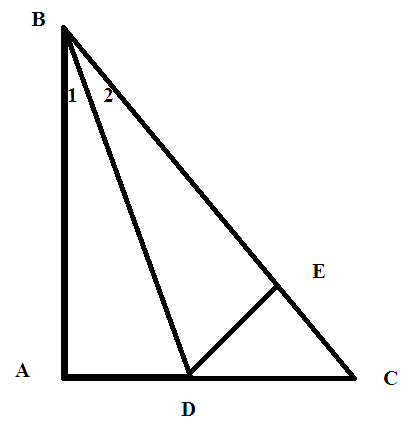
Xét △BAD và △ BED có:

\(\widehat{A}=\widehat{AED}=90^o\)

\(\widehat{B_1}=\widehat{B_2}\)

AD chung

Nên △BAD= và △ BED (g.c.g)

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có

góc HBA chung

=>ΔHBA đồng dạng với ΔABC

b; Xét ΔABE vuông tại A và ΔACB vuông tại A có

góc ABE=góc ACB

=>ΔABE đồng dạng với ΔACB

=>AB/AC=AE/AB

=>AB^2=AE*AC

c: Xét ΔBHD vuông tại H và ΔBAE vuông tại A có

góc HBD=góc ABE

=>ΔBHD đồng dạng với ΔBAE

Áp dụng ddL pytago vào Δ abc( góc a =90 )

BC² =AB² +AC²

⇒BC²=16+9=25

⇒BC=5

Xét Δabc vông tại a có:

AH=\(\dfrac{1}{2}\) BC=\(\dfrac{5}{2}\) =2.5 (CM)

Vậy AH=2.5cm

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(AB^2+AC^2=BC^2\)

\(\Leftrightarrow AC^2=BC^2-AB^2=5^2-3^2=16\)

hay AC=4(cm)

Vậy: AC=4cm

b) Xét ΔABD vuông tại A và ΔEBC vuông tại E có 

\(\widehat{ABD}=\widehat{EBC}\)(BE là tia phân giác của \(\widehat{ABC}\))

Do đó: ΔABD\(\sim\)ΔEBC(g-g)