Tọa độ giao điểm của đường thẳng (d₁) và (d₂) là:
\(\left\{{}\begin{matrix}-2x+5y-8=0\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)

Để 3 đường thẳng trên đồng qua thì:

\(\left(m^2-1\right)x+3y-5-2m=0\\ \Leftrightarrow\left(m^2-1\right).1+3.2-5-2m=0\\ \Leftrightarrow m^2-1+6-5-2m=0\\ \Leftrightarrow m^2-2m=0\\ \Leftrightarrow m\left(m-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}m=0\\m=2\end{matrix}\right.\)

Tọa độ giao điểm của (d1) và (d2) là:

\(\left\{{}\begin{matrix}-2x+5y-8=x+2y-5\\x+2y-5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y=1\\x+2y=5\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)

Thay x=1 và y=2 vào (d3), ta được:

\(m^2-1+3\cdot2-5-2m=0\)

\(\Leftrightarrow m\left(m-2\right)=0\)

hay \(m\in\left\{0;2\right\}\)

Để hai đường song song thì m=2 và m-1=1 và m<>-1

=>m=2

a) Lấy hai điểm A(0;4) và B(2;0) thuộc d. Gọi A′, B′ theo thứ tự là ảnh của A và B qua phép vị tự tâm O tỉ số k = 3. Khi đó ta có

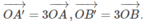
Vì  O A →   =   ( 0 ; 4 ) nên  O A ' →   =   ( 0 ; 12 ) . Do đó A′ = (0;12).

Tương tự B′ = (6;0); d1 chính là đường thẳng A'B' nên nó có phương trình:

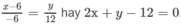
b) Có thể giải tương tự như câu a) .

Sau đây ta sẽ giải bằng cách khác.

Vì d 2   / /   d nên phương trình của d 2  có dạng 2x + y + C = 0.

Gọi A′ = (x′;y′) là ảnh của A qua phép vị tự đó thì ta có:

I A ' →   =   − 2 I A →  hay x′ + 1 = −2, y′ − 2 = −4

Suy ra x′ = −3, y′ = −2

Do A' thuộc d 2  nên 2.(−3) – 2 + C = 0.

Từ đó suy ra C = 8

Phương trình của d 2  là 2x + y + 8 = 0

Chọn A