Tìm điều kiện xác định của mỗi phương trình sau:
a) \(\frac{{3x + 1}}{{2x - 1}} = 1;\)
b) \(\frac{x}{{x - 1}} + \frac{{x + 1}}{x} = 2.\)
Những câu hỏi liên quan
Điều kiện xác định của phương trình \(\dfrac{2x+1}{x-1}+\dfrac{2-3x}{1+x}=\dfrac{1}{2}\)
Điều kiện xác định của phương trình
1
x
-
1
+
2
x
-
2
+
3
x
-
3
6
x
-
6
là A. x ≠ 1 B. x ≠ 2, x ≠ 3. C. x ≠ 1, x ≠ 2, x ≠ 3. D. x ≠ 1, x ≠ 2, x ≠ 3, x ≠ 6.
Đọc tiếp
Điều kiện xác định của phương trình 1 x - 1 + 2 x - 2 + 3 x - 3 = 6 x - 6 là
A. x ≠ 1
B. x ≠ 2, x ≠ 3.
C. x ≠ 1, x ≠ 2, x ≠ 3.
D. x ≠ 1, x ≠ 2, x ≠ 3, x ≠ 6.
Chọn D
Điều kiện để phương trình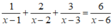 
xác định là:
x – 1 ≠ 0 và x - 2 ≠ 0 và x – 3 ≠ 0 và x – 6 ≠ 0 ⇔ x ≠ 1, x ≠ 2, x ≠ 3, x ≠ 6
Đúng 0
Bình luận (0)
Cho phương trình, tìm điều kiện xác định của phương trình sau
2
x
+
1
x
2
-
4
+
2
x
+
1
3
2
-
x
A.
x
≠
±
2
B.
x
≠
-...
Đọc tiếp
Cho phương trình, tìm điều kiện xác định của phương trình sau 2 x + 1 x 2 - 4 + 2 x + 1 = 3 2 - x
A. x ≠ ± 2
B. x ≠ - 1
C. x ≠ ± 2 , x ≠ - 1
D. x ≠ 2
Tìm điều kiện xác định của các phương trình sau ( x - 1 ) ( 1 - 2 x ) = 1
Ta thấy 1 - 2x ≠ 0 khi x ≠ 1/2.
Do đó ĐKXĐ của phương trình (x - 1)/(1 - 2x) = 1 là x ≠ 1/2.
Đúng 0
Bình luận (0)
8 tháng 5 2023 lúc 19:45
tìm điều kiện xác định của phương trình 1/2x^2+1 = x - 3
Tìm điều kiện xác định của phương trình sau:
3
x
-
2
2
x
-
1
x
-
2
-
x
Đọc tiếp
Tìm điều kiện xác định của phương trình sau:
3 x - 2 = 2 x - 1 x - 2 - x
x – 2 ≠ 0 khi x ≠ 2
Vậy ĐKXĐ của phương trình là x ≠ 2.
Đúng 0
Bình luận (0)
Tìm điều kiện của mỗi phương trình sau: - 3 x + 2 = 2 x + 1
tìm điều kiện xác định của các phương trình saua,3x^2-2x0 b,dfrac{1}{x-1}3c,dfrac{2}{x-1}dfrac{x}{2x-4} d,dfrac{2x}{x^2-9}dfrac{1}{x+3}e,2xdfrac{1}{x^2-2x+1} f,dfrac{1}{x-2}dfrac{2x}{x^2-5x+6} giúp mik với , mik cần gấp
Đọc tiếp
tìm điều kiện xác định của các phương trình sau
\(a,3x^2-2x=0\) \(b,\dfrac{1}{x-1}=3\)
\(c,\dfrac{2}{x-1}=\dfrac{x}{2x-4}\) \(d,\dfrac{2x}{x^2-9}=\dfrac{1}{x+3}\)
\(e,2x=\dfrac{1}{x^2-2x+1}\) \(f,\dfrac{1}{x-2}=\dfrac{2x}{x^2-5x+6}\)
giúp mik với , mik cần gấp
a)\(x\in R\)
b)\(x\ne1\)
c) \(x\notin\left\{1;2\right\}\)
d) \(x\notin\left\{3;-3\right\}\)
e) \(x\ne1\)
f) \(x\notin\left\{2;3\right\}\)
Đúng 0
Bình luận (2)
a) x∈R
b) x≠1
c) x∉{1;2}
d) x∉{3;−3}
e) x≠1
f) x∉{2;3}
Đúng 2
Bình luận (0)
tìm điều kiện xác định
giải phương trình
\(\sqrt{\frac{3x-2}{x+1}}=3\)
ĐKXĐ: \(\hept{\begin{cases}x\ne-1\\\frac{3x-2}{x+1}\ge0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne-1\\\orbr{\begin{cases}x\ge\frac{3}{2}\\x\le-1\end{cases}}\end{cases}}}\)
Khi đó: \(\sqrt{\frac{3x-2}{x+1}}=3\)
\(\Leftrightarrow\frac{3x-2}{x+1}=9\)
\(\Leftrightarrow9x+9=3x-2\)
\(\Leftrightarrow6x=-11\)
\(\Leftrightarrow x=\frac{-11}{6}\)(T/m ĐKXĐ)
ĐKXĐ: \(\hept{\begin{cases}x\ne-1\\x\ge\frac{3}{2}hoặcx\le-1\end{cases}}\)
![Yuri Sweet[𝕿𝖊𝖆𝖒 𝕹𝖊𝖕𝖆𝖑]](https://hoc24.vn/images/avt/avt6428199_256by256.jpg)
ĐKXĐ : \(\orbr{\begin{cases}x\ge\frac{2}{3}\\x\le-1\end{cases}}\)
Ta có : \(\sqrt{\frac{3x-2}{x+1}}=3\)
\(\Leftrightarrow\frac{3x-2}{x+1}=9\)
\(\Leftrightarrow3x-2=9\left(x+1\right)\)
\(\Leftrightarrow3x-2=9x+9\)
\(\Leftrightarrow6x=-11\)
\(\Leftrightarrow x=-\frac{11}{6}\left(TM\right)\)
Vậy PT có 1 nghiệm duy nhất là \(x=-\frac{11}{6}\)
Tìm điều kiện của mỗi phương trình sau: 3 x + 5 3 x 2 + 6 x + 11 = 2 x + 1
3 x 2 + 6 x + 11 = 0 và x ≥ -1/2. Vì ta có 3 x 2 + 6 x + 11 = 3 ( x + 1 ) 2 + 8 > 0 với mọi x, nên điều kiện của phương trình là x ≥ -1/2
Đúng 0
Bình luận (0)