\(\left\{{}\begin{matrix}\left(x+1\right)\left(y-1\right)=xy-1\\\left(x-3\right)\left(y-3\right)=xy-3\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}xy-x+y-1=xy-1\\xy-3x-3y+9=xy-3\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}-x+y=0\\-3x-3y=-12\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}-x+y=0\\x+y=4\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}2y=4\\x+y=4\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=2\\x+2=4\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}y=2\\x=2\end{matrix}\right.\)

Vậy (2;2) là nghiệm

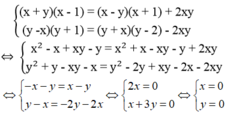
Vậy nghiệm của hệ phương trình là (x; y) = (0; 0)

x^2+xy+y^2=19(1)

x-xy+y=-1(2) =>x=xy-1-y(4)

Cộng (1) cho (2) ta dc x^2+y^2+x+y=18(3)

thay (4) vào (3) ta dc (xy-1-y)^2+y^2+(xy-1-y)+y=18(5)

18(5)

duyện đi

`x-y=2<=>x=y+2` thay vào trên
`=>m(y+2)+2y=m+1`
`<=>y(m+2)=m+1-2m`
`<=>y(m+2)=1-2m`
Để hpt có nghiệm duy nhất
`=>m+2 ne 0<=>m ne -2`
`=>y=(1-2m)/(m+2)`
`=>x=y+2=5/(m+2)`
`xy=x+y+2`
`<=>(5-10m)/(m+2)=(6-2m)/(m+2)+2`
`<=>(5-10m)/(m+2)=10/(m+2)`
`<=>5-10m=10`
`<=>10m=-5`
`<=>m=-1/2(tm)`
Vậy `m=-1/2` thì HPT có nghiệm duy nhât `xy=x+y+2`

`a)m=2`

$\begin{cases}2x+2y=3\\x-y=2\end{cases}$
`<=>` $\begin{cases}2x+2y=3\\2x-2y=4\end{cases}$
`<=>` $\begin{cases}4y=-1\\x=y+2\end{cases}$
`<=>` $\begin{cases}y=-\dfrac14\\y=\dfrac74\end{cases}$
Vậy m=2 thì `(x,y)=(7/4,-1/4)`

Sửa đoạn `xy=x+y+2`

``<=>(5-10m)/(m+2)^2=(6-2m)/(m+2)+2`
`<=>(5-10m)/(m+2)^2=10/(m+2)`

`<=>5-10m=10(m+2)`

`<=>1-2m=2m+4`

`<=>4m=-3`

`<=>m=-3/4(tm)`

a)\(\hept{\begin{cases}x+y+xy=11\\x^2y+xy^2=30\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y+xy=11\\xy\left(x+y\right)=30\end{cases}}\)

Đặt \(S=x+y;P=xy\left(S^2\ge4P\right)\) có:

\(\hept{\begin{cases}S+P=11\\SP=30\end{cases}}\Rightarrow\hept{\begin{cases}S=5\\P=6\end{cases}}or\hept{\begin{cases}S=6\\P=5\end{cases}}\)

\(\Rightarrow\hept{\begin{cases}x+y=6\\xy=5\end{cases}or\hept{\begin{cases}x+y=5\\xy=6\end{cases}}}\)

\(\Rightarrow\hept{\begin{cases}x=1\\y=5\end{cases};\hept{\begin{cases}x=5\\y=1\end{cases}}or\hept{\begin{cases}x=2\\y=3\end{cases}};\hept{\begin{cases}x=3\\y=2\end{cases}}}\)

b)Thay số hay đặt ẩn.... gì đó tùy, nhiều pp 

ra \(x=8;y=-8\)

ĐKXĐ : \(x;y\ne0\)

Khi đó \(\left\{{}\begin{matrix}x-\dfrac{1}{x}=y-\dfrac{1}{y}\\2x^2-xy=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y=-\dfrac{x-y}{xy}\\2x^2-xy=1\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y\right)\left(\dfrac{xy+1}{xy}\right)=0\\2x^2-xy=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x=y\\xy=-1\end{matrix}\right.\\2x^2-xy=1\end{matrix}\right.\)

Với x = y thì 2x² - xy  = 1

<=> 2x² - x² = 1

<=> x² = 1

<=> x = \(\pm1\) (tm) 

Khi x = -1 => y = -1

x = 1 => y = 1

Với xy = - 1 thì 2x² - xy = 1

<=> 2x² - (-1) = 1

<=> x² = 0

<=> x = 0 (ktm) 

Vậy hệ có 2 nghiệm (x;y) = (1; 1) ; (-1 ; -1)