tính góc giữa các cặp đường thẳng sau : a,(d1)5x+3y-1=0;(d2):x+2y+2=0

Những câu hỏi liên quan
Góc giữa 2 đường thẳng d1:x+3y-3=0 và d2: x+√3y +2=0
\(d_1\) nhận \(\overrightarrow{n_1}=\left(1;3\right)\) là 1 vtpt
\(d_2\) nhận \(\overrightarrow{n_2}=\left(1;\sqrt{3}\right)\) là 1 vtpt
Gọi \(\alpha\) là góc giữa d1 và d2
\(\Rightarrow cos\alpha=\left|cos\left(\overrightarrow{n_1};\overrightarrow{n_2}\right)\right|=\dfrac{\left|1.1+3.\sqrt{3}\right|}{\sqrt{1^2+3^2}.\sqrt{1^2+3}}=\dfrac{3\sqrt{3}+1}{2\sqrt{10}}\)
\(\Rightarrow\alpha\approx11^034'\)
Đúng 0
Bình luận (0)
Cho điểm A(1; 3) và hai đường thẳng
d
1
:
2
x
−
3
y
+
4
0
,
d
2
:
3
x
+
y
0
. Số đường thẳng qua A và tạo với
d
1
,
d
2
các góc bằng nhau là A.1 B.2 C.4 D.Vô số
Đọc tiếp
Cho điểm A(1; 3) và hai đường thẳng d 1 : 2 x − 3 y + 4 = 0 , d 2 : 3 x + y = 0 . Số đường thẳng qua A và tạo với d 1 , d 2 các góc bằng nhau là
A.1
B.2
C.4
D.Vô số
ĐÁP ÁN B
Đường thẳng qua A và tạo với d1d2 các góc bằng nhau khi vuông góc với phân giác của góc tạo bởi d1d2.
Do vậy số lượng đường thẳng cần tìm là 2.
Đúng 0
Bình luận (0)
Tìm số đo của góc giữa hai đường thẳng d1 và d2 lần lượt có phương trình: d1: 4x – 2y + 6 = 0 và d2: x – 3y + 1 = 0
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
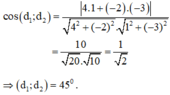
Đúng 2
Bình luận (0)
Lập phương trình đường phân giác của các góc giữa hai đường thẳng sau
a) (d1) : 2x+4y+7=0 và (d2) : 5x+3y+7=0
b) (d1) : -3x+4y+8=0 và (d2) : x-y+6 = 0
Hai câu tương tự, mình làm câu a:
Gọi \(M\left(x;y\right)\) là điểm thuộc đường phân giác của 2 đường thẳng
Theo tính chất phân giác ta có:
\(d\left(M;d_1\right)=d\left(M;d_2\right)\)
\(\Leftrightarrow\frac{\left|2x+4y+7\right|}{\sqrt{2^2+4^2}}=\frac{\left|5x+3y+7\right|}{\sqrt{5^2+3^2}}\)
\(\Leftrightarrow\sqrt{34}\left|2x+4y+7\right|=2\sqrt{5}\left|5x+3y+7\right|\)
\(\Rightarrow\left[{}\begin{matrix}\sqrt{34}\left(2x+4y+7\right)=2\sqrt{5}\left(5x+3y+7\right)\\\sqrt{34}\left(2x+4y+7\right)=-2\sqrt{5}\left(5x+3y+7\right)\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left(2\sqrt{34}-10\sqrt{5}\right)x+\left(4\sqrt{34}-6\sqrt{5}\right)y+7\sqrt{34}-14\sqrt{5}=0\\\left(2\sqrt{34}+10\sqrt{5}\right)x+\left(4\sqrt{34}+6\sqrt{5}\right)y+7\sqrt{34}+14\sqrt{5}=0\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°
Xem thêm câu trả lời
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là:
A. 9x + 7y + 2 = 0 và 7x – 9y = 0
B. 9x – 7y + 2 = 0 và 77x – 99y + 46 = 0
C. 9x – 7y + 2 = 0 và 7x + 9y = 0
D. 9x + 7y + 2 = 0 và 77x – 99y + 46 = 0
Quỹ tích các điểm cách đều hai đường thẳng d1: 5x-12y+4=0, d2: 4x-3y+2=0 là hai đường phân giác ∆1,2 của chúng
Phương trình ∆1 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = 52 x − 39 y + 26 ⇔ − 27 x − 21 y − 6 = 0 ⇔ 9 x + 7 y + 2 = 0
Phương trình ∆2 là
5 x − 12 y + 4 5 2 + ( − 12 ) 2 = − 4 x − 3 y + 2 4 2 + ( − 3 ) 2 ⇔ 5 x − 12 y + 4 13 = − 4 x − 3 y + 2 5 ⇔ 5 ( 5 x − 12 y + 4 ) = − 13 ( 4 x − 3 y + 2 ) ⇔ 25 x − 60 y + 20 = − 52 x + 39 y − 26 ⇔ 77 x − 99 y + 46 = 0
Đáp án D
Đúng 0
Bình luận (0)
Cho ba đường thẳng
d
1
:
3
x
−
4
y
+
1
0
,
d
2
:
5
x
+
3
y
−
1
0
,
d
3
:
x
+
y
+
6
0
. Số điểm M cách đều ba đường thẳng trên...
Đọc tiếp
Cho ba đường thẳng d 1 : 3 x − 4 y + 1 = 0 , d 2 : 5 x + 3 y − 1 = 0 , d 3 : x + y + 6 = 0 . Số điểm M cách đều ba đường thẳng trên là
A.1
B. 2
C.3
D. 4
Do các đường thẳng đôi một cắt nhau tại các điểm A, B, C nên các điểm cách đều các cạnh gồm tâm đường tròn nội tiếp và ba tâm đường tròn bàng tiếp.
Vậy có tất cả 4 điểm M cách đều ba đường thẳng đã cho.
đáp án D
Đúng 0
Bình luận (0)
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
Tính góc giữa hai đường thẳng
∆
:
x
-
3
y
+
2
0
và
∆
:
x
+
3
y
-
1
0
A.
90
0
B.
120
0
C.
60
0
D.
30...
Đọc tiếp
Tính góc giữa hai đường thẳng ∆ : x - 3 y + 2 = 0 và ∆ ' : x + 3 y - 1 = 0
A. 90 0
B. 120 0
C. 60 0
D. 30 0















