Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
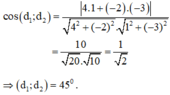
Với d1: 4x – 2y + 6 = 0 có vecto pháp tuyến là: n1→(4;-2)
và d2: x – 3y + 1 = 0 có vecto pháp tuyến là: n2→(1;-3) ; ta có :
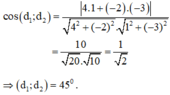
Cho hai đường thẳng d1 : x+ 2y -1 = 0 và d2 : x- 3y +3 = 0. Phương trình đường thẳng d đối xứng với d1 qua là: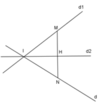
A. x -3y- 2= 0
B.x+ 3y+1= 0
C. 3x-y=1= 0
D. x-3y+ 3=0
Cho hai đường thẳng d1: 2x + 2 3 y + 5 = 0 và d2: y - 6 = 0. Góc giữa d1 và d2 có số đo bằng:
A. 30 °
B. 45 °
C. 60 °
D. 135 °
Cho d1:2x+5y+4=0 và d2:5x-2y+6=0.Số đo của góc giữa 2 đường thẳng d1 và d2 là? A.90° B.60° C.45° D.30°
cho 2 đường thẳng d1: x + 2y + 4 = 0; d2: 2x - y + 6 = 0. Số đo góc giữa d1; d2 là:
A. 300
B. 600
C. 450
D. 900
Cho hai đường thẳng d1 : x+ y -1= 0 và d2 : x- 3y + 3= 0. Phương trình đường thẳng d đối xứng với d1 qua đường thẳng d2 là:
A.x-7y +1 =0
B.x+7y +1= 0
C. 7x+y+1= 0
D. 7x-y+1= 0
Viết phương trình đường thẳng d đối xứng qua d1 qua d2 biết d1:x+2y-1=0,d2 : x-3y+3=0
Cho tam giác ABC có A(2;−1). Đường phân giác trong góc B và C có phương trình lần
lượt là d1 :x−2y+1=0 và d2 :x+y+3=0. Viết phương trình đường thẳng chứa các cạnh của tam giác ABC.
Lập phương trình của đường thẳng ∆ đi qua giao điểm của hai đường thẳng d1: x + 3y – 1 =0 d2: x – 3y - 5= 0 và vuông góc với đường thẳng d3: 2x - y + 7 = 0.
A. 3x + 6y - 5=0.
B. 6x + 12y - 5 = 0.
C. 6x+ 12y + 10 = 0.
D. x +2y + 10 = 0.
Lập phương trình đường tròn có tâm nằm trên đường thẳng Δ: 4x + 3y – 2 = 0 và tiếp xúc với hai đường thẳng d1: x + y + 4 = 0 và d2: 7x – y + 4 = 0 .