Phân tích dùm em bài này với ạ. Em cảm ơn trước ạ

Những câu hỏi liên quan
Ai giải dùm em bài này em cảm ơn ạ!

làm giúp em bài này với ạ em cảm ơn trước ạ
1. What size shoes do you take?
2. What newspaper do you read?
3. What color are your eyes?
4. What time did you arrive this morning?
5. What kind of film do you like?
6. How tall is your teacher?
7. How far is it from your house to the office?
8. How much did you pay for your new shirt?
9. How often do you take an English test in class?
10. How long have you been studying English?
Đúng 0
Bình luận (0)
giúp em vài bài này với ạ em cảm ơn mn trước ạ

Mọi người giúp em 3 bài này với ạ! em đang cần gấp!!!
Cảm ơn trước ạ.
Giúp em hoàn thành mấy bài này trước 19h với ạ! Em cảm ơn!https://hoc24.vn/vip/278208647180Giúp em với ạ!
Đọc tiếp




Giúp em hoàn thành mấy bài này trước 19h với ạ!
Em cảm ơn!
https://hoc24.vn/vip/278208647180
Giúp em với ạ!
Bài 1:
1) Ta có: \(M=\left(\dfrac{\sqrt{a}}{\sqrt{a}-1}-\dfrac{1}{a-\sqrt{a}}\right):\left(\dfrac{1}{\sqrt{a}+1}+\dfrac{2}{a-1}\right)\)
\(=\dfrac{a-1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{\sqrt{a}-1+2}{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}\)
\(=\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}+1\right)}{\sqrt{a}+1}\)
\(=\dfrac{a-1}{\sqrt{a}}\)
2) Thay \(a=3-2\sqrt{2}\) vào M, ta được:
\(M=\dfrac{3-2\sqrt{2}-1}{\sqrt{2}-1}=\dfrac{-2\sqrt{2}+2}{\sqrt{2}-1}\)
\(=\dfrac{-2\left(\sqrt{2}-1\right)}{\sqrt{2}-1}=-2\)
Đúng 0
Bình luận (0)

 giải chi tiết 3 bài này dùm em vs ạ
giải chi tiết 3 bài này dùm em vs ạ
em cảm ơn mọi người nhiều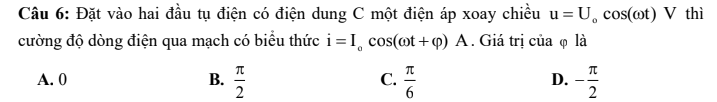
Giải dùm em hệ phương trình này với ạ!
em cảm ơn
Lấy \(2.\left(2\right)-\left(1\right)\) ta được:
\(2b+4a+6-\left(a-1-2b\right)=0\)
\(\Leftrightarrow4b+3a+7=0\Rightarrow b=\dfrac{-3a-7}{4}\)
Thế vào (2):
\(\sqrt{a^2+\left(\dfrac{-3a-7}{4}\right)^2}=\dfrac{-3a-7}{4}+2a+3\)
\(\Leftrightarrow\sqrt{25a^2+42a+49}=5a+5\) (\(a\ge-1\))
\(\Leftrightarrow25a^2+42a+49=25a^2+50a+25\)
\(\Rightarrow a=...\Rightarrow b=...\)
Đúng 0
Bình luận (0)
Giải dùm em bài 9 với ạ em cảm ơn
9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)
Đúng 1
Bình luận (1)
giúp em vài bài này với ạ em cảm ơn mn trước ạ
giuớ đi mòa :(

13:
a vuông góc HK
b vuông góc HK
Do đó: a//b
12: góc x'AB=góc ABy
mà hai góc này là hai góc ở vị trí so le trong
nên xx'//y'y
Đúng 0
Bình luận (0)
















