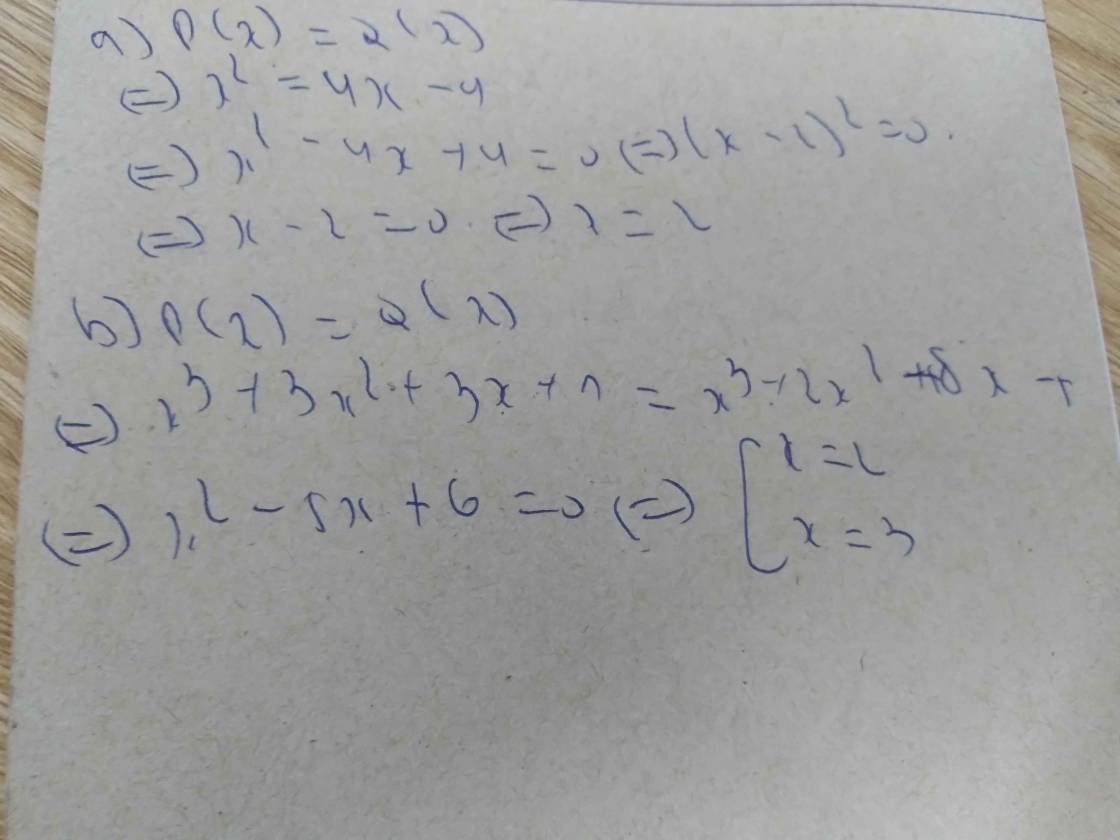cho A = x^2 - 3x. Hỏi với giá trị nào của x thì: A=0; A>0; A<0

Những câu hỏi liên quan
Bài 1: Cho A= x(x-4). Với giá trị nào của x thì: A=0; A<0; A>0
Bài 2: Cho B= (x-3) : x (x khác 0). Với giá trị nào của x thì: B=0 ; B<0; B>0
Cho biểu thức:
\(A=\left(\frac{x^2}{x^3-4x} +\frac{6}{6-3x}+\frac{1}{x+2}\right):\left(x-2+\frac{10-x^2}{x+2}\right)\)
a) Rút gọn A
b) Tìm giá trị của biểu thức khi /x/=\(\frac{1}{2}\)
c) Với giá trị nào của x thì A=2
d) Với giá trị nào của x thì A<0
e) Tìm giá trị nguyên của x để A nhận giá trị nguyên
cho biểu thức A=\(\sqrt{\left[3x+1\right]\left[x-2\right]}\)và B=\(\sqrt{3x+1}.\sqrt{x-2}\)với giá trị nào của x thì A=B,với giá trị nào của x thì chỉ A có nghĩa còn B không có nghĩa
giúp mk vs m.n, HELP ME! THANK YOU.Câu 1/ Cho hai tập hợp A {x ∈ R | (2x - x2)(2x2 - 3x -) 0} và B {x ∈ R | (2x2 + x)(3x - 12m) 0}. Với giá trị nào của m thì A B?Câu 2/ Cho các tập hợp A [1 ; +∞), B {x ∈ R | x2 + 1 0} và C (0;4). Tập (A hợp B) giao C. Có bao nhiêu phần tử số nguyên.Câu 3/ Cho hai tập hợp A (m-1 ; 5], B (3; 2020 - 5m) và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để A B ∅
Đọc tiếp
giúp mk vs m.n, HELP ME! THANK YOU.
Câu 1/ Cho hai tập hợp A = {x ∈ R | (2x - x2)(2x2 - 3x -) = 0} và B = {x ∈ R | (2x2 + x)(3x - 12m) = 0}. Với giá trị nào của m thì A = B?
Câu 2/ Cho các tập hợp A = [1 ; +∞), B = {x ∈ R | x2 + 1 = 0} và C = (0;4). Tập (A hợp B) giao C. Có bao nhiêu phần tử số nguyên.
Câu 3/ Cho hai tập hợp A= (m-1 ; 5], B = (3; 2020 - 5m) và A, B khác rỗng. Có bao nhiêu giá trị nguyên của m để A \ B = ∅
Câu 2:
\(\left(A\cup B\right)\cap C=A\cap C=[1;+\infty)\cap\left(0;4\right)=[1;4)\)
Tập này có 3 phần tử nguyên
Đúng 0
Bình luận (0)
cho biểu thức F=8-2x/3x+2
a)Với giá trị nào của x thì biểu thức trên xác định.
b)Với giá trị nào của x thì biểu thức F=0.
c) Tìm x nguyên để F có giá trị nguyên.
d) Tìm x để F<0 .
a: ĐKXĐ: x<>-2/3
b: F=0
=>8-2x=0
=>x=4
d: F<0
=>(2x-8)/(3x+2)>0
=>x>4 hoặc x<-2/3
Đúng 0
Bình luận (0)
Với giá trị nào của x thì đồ thị hàm số y = 2 / 3 x nằm phía trên đường thẳng y = 1?
A. x > 0 B. x < 0
C. x = 0 D. x < 1
a) cho 2 đa thức P(x)=x2 và đa thức Q(x)=4x-4. với giá trị nào của x thì P(x)=Q(x)
b) a) cho 2 đa thức P(x)=x3+3x2+3x+1 và đa thức Q(x)=x3+2x2+8x-5. với giá trị nào của x thì P(x)=Q(x)Cho hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x + a}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + b}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
a) Với \(a = 0,b = 1\), xét tính liên tục của hàm số tại \(x = 2\).
b) Với giá trị nào của a, b thì hàm số liên tục tại \(x = 2\) ?
c) Với giá trị nào của a, b thì hàm số liên tục trên tập xác định?
Với a = 0, b = 1, hàm số \(f(x) = \left\{ {\begin{array}{*{20}{l}}{2x}&{{\rm{ }}x < 2}\\4&{{\rm{ }}x = 2}\\{ - 3x + 1}&{{\rm{ }}\,x > 2}\end{array}} \right.\)
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + 1} \right) = - 3.2 + 1 = - 5\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x} \right) = 2.2 = 4\\ \Rightarrow \mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) \ne \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right)\end{array}\)
Do đó không tồn tại giới hạn \(\mathop {\lim }\limits_{x \to 2} f\left( x \right)\)
Vậy hàm số không liên tục tại x = 2.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} \left( { - 3x + b} \right) = - 3.2 + b = - 6 + b\\\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ - }} \left( {2x + a} \right) = 2.2 + a = 4 + a\\f\left( 2 \right) = 4\end{array}\)
Để hàm số liên tục tại x = 2 thì \(\mathop {\lim }\limits_{x \to {2^ - }} f\left( x \right) = \mathop {\lim }\limits_{x \to {2^ + }} f\left( x \right) = f\left( 2 \right)\)
\( \Leftrightarrow - 6 + b = 4 + a = 4 \Leftrightarrow \left\{ \begin{array}{l}4 + a = 4\\ - 6 + b = 4\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}a = 0\\b = 10\end{array} \right.\)
Vậy với a = 0 và b = 10 thì hàm số liên tục tại x = 2.
c) Tập xác định của hàm số là: ℝ.
Với x < 2 thì \(f\left( x \right) = 2x + a\) là hàm đa thức nên liên tục.
Với x > 2 thì \(f\left( x \right) = -3x + b\) là hàm đa thức nên liên tục.
Do đó để hàm số liên tục trên ℝ thì hàm số \(f\left( x \right)\) liên tục tại x = 2.
Vậy với a = 0 và b = 10 thỏa mãn điều kiện.
Đúng 0
Bình luận (0)
1. với giá trị nào của x thì đa thức dư trong mỗi phép chia sau có giá trị bằng 0
a) (2x^4-3x^3+4x^2+1) : (x^2-1)
b) (x^5+2x^4+3x^4+x-3) : (x^2+1)