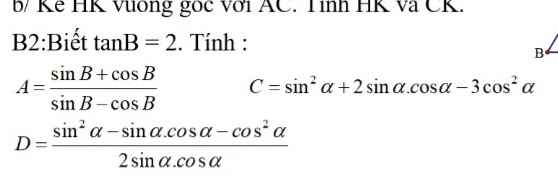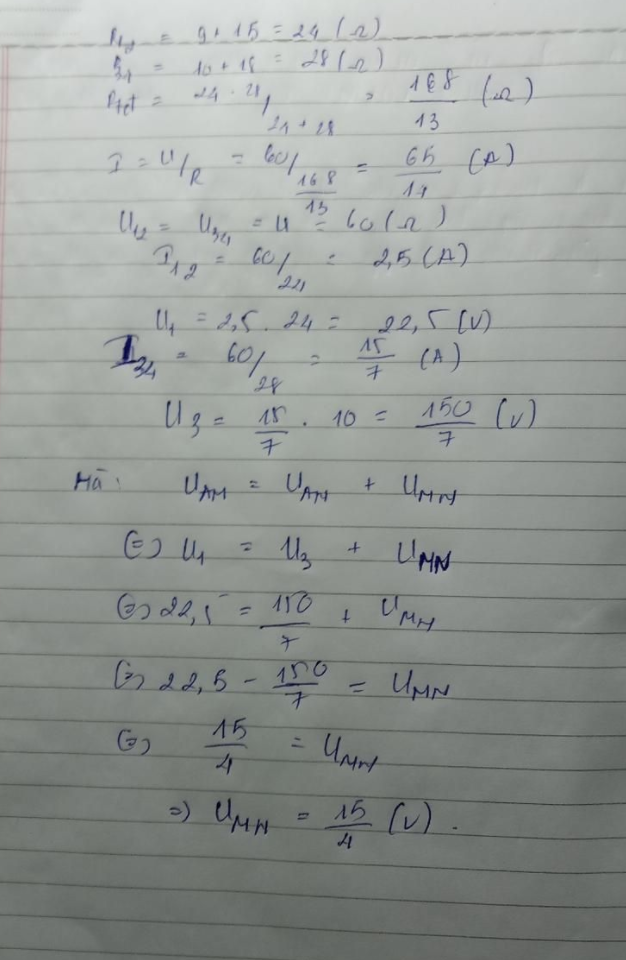cho em xin hình bài này vs ạ,e đang cần gấp ạ

Những câu hỏi liên quan
Giúp e vs ạ, e đang cần gấp lắm. EM XIN LỖI VÌ HƠI MỜ Ạ, E XIN CẢM ƠN
Giúp e vs ạ, em đang cần rất gấp, EM XIN CẢM ƠN ANH CHỊ Ạ!
Các anh chị em giúp em cái này vs ạ e đang cần lời giới thiệu trong buổi diễn văn nghệ nhân dịp 20 - 11 cho bài vui đến trường cần gấp hôm nay ai giúp đỡ em vs ạ
Giúp em giải bài này vs ạ em đang cần gấp ạ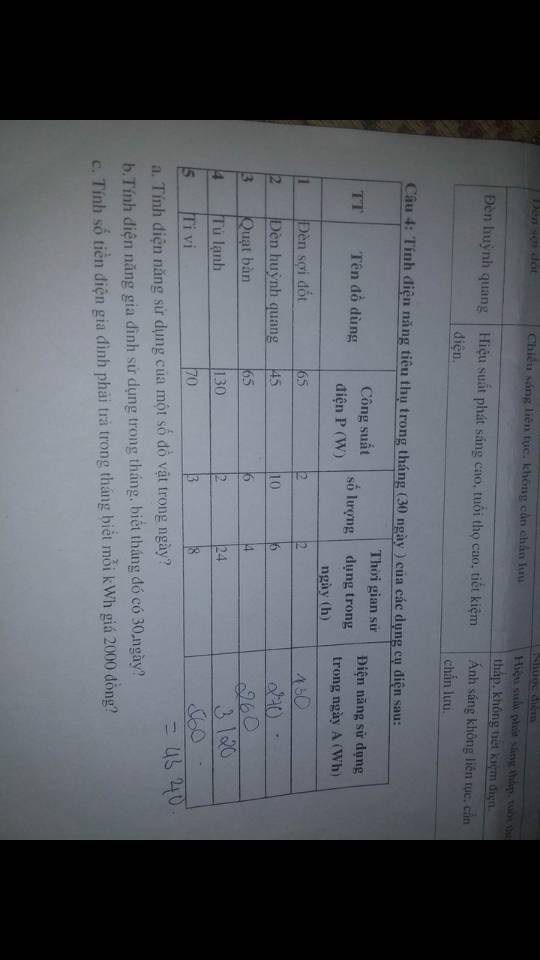
Giúp mik bài này vs ạ, chỉ cần cậ d thôi ạ( mn giúp em vs em đang cần gấp )
a/ Tam giác AMN cân tại A (gt). \(\Rightarrow\) \(\widehat{AMN}=\widehat{ANM};AM=AN.\)
Xét tam giác AMB và tam giác ANC có:
+ AM = AN (cmt).
+ \(\widehat{AMB}=\widehat{ANC}\left(\widehat{AMN}=\widehat{ANM}\right).\)
+ MB = NC (gt).
\(\Rightarrow\) Tam giác AMB = Tam giác ANC (c - g - c).
\(\Rightarrow\) AB = AC (cặp cạnh tương ứng).
Xét tam giác ABC có: AB = AC (cmt).
\(\Rightarrow\) Tam giác ABC cân tại A.
b/ Tam giác ABC cân tại A (cmt) \(\Rightarrow\) \(\widehat{ABC}=\widehat{ACB}.\)
Mà \(\widehat{ABC}=\widehat{MBH;}\widehat{ACB}=\widehat{NCK}\text{}\) (đối đỉnh).
\(\Rightarrow\) \(\widehat{MBH}=\widehat{NCK}.\)
Xét tam giác MBH và tam giác NCK \(\left(\widehat{BHM}=\widehat{CKN}=90^o\right)\)có:
+ MB = NC (gt).
+ \(\widehat{MBH}=\widehat{NCK}\left(cmt\right).\)
\(\Rightarrow\) Tam giác MBH = Tam giác NCK (cạnh huyền - góc nhọn).
c/ Tam giác MBH = Tam giác NCK (cmt).
\(\Rightarrow\) \(\widehat{BMH}=\widehat{CNK}\) (cặp góc tương ứng).
Xét tam giác OMN có: \(\widehat{NMO}=\widehat{MNO}\) (do \(\widehat{BMH}=\widehat{CNK}\)).
\(\Rightarrow\) Tam giác OMN tại O.
Đúng 0
Bình luận (0)
Xin mọi người giúp vs ạ, em đang cần gấp lắm ạ.Nếu đc cho em xin cả cách giải ạ


Câu 1: A
Câu 2: B
Câu 3: D
Câu 4: A
Câu 5: C
Câu 6: B
Đúng 1
Bình luận (0)
Giải giúp e bài hình này với ạ
E đang cần gấp ạ , e cảm ơn

a: Xét ΔHAC vuông tại H và ΔABC vuông tại A có
\(\widehat{C}\) chung
Do đó: ΔHAC~ΔABC
b: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=15^2+20^2=625\)
=>BC=25
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}BH\cdot BC=BA^2\\AH\cdot BC=AB\cdot AC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH\cdot25=15^2=225\\AH\cdot25=15\cdot20=300\end{matrix}\right.\)
=>BH=9; AH=12
Đúng 0
Bình luận (0)
Cho hình vuông ABCD có cạnh bằng 8,1 cm . Trên AB lấy điểm M sao cho AM =1/3 AB . Trên BC lấy điểm N sao cho BN=2/3 BC.
a) Tính diện tích tam giác DMN .
b) MN và BD cắt nhau tại E . So sánh độ dài hai đoạn thẳng EM và EN .
mn giúp em bài này vs ạ , e đang cần rất gấp . e lm đc phần a rồi chỉ còn phần b thôi ạ . Em xin cảm ơn.
a) Diện tích hình vuông ABCD là :
8,1 x 8,1 = 65,61 ( cm2 )
Vì AM = 1/3 AB nên MB gấp 2 lần AM
=> MB là : 8,1 : 3 x 2 = 5,4 ( cm )
Vì BN = 2/3 BC nên NC gấp 2 lần BN
=> BN là : 8,1 : 3 x 1 = 2,7 ( cm )
Diện tích tam giác BMN là :
5,4 x 2,7 : 2 = 7,29 ( cm2 )
AM = 8,1 : 3 x 1 = 2,7 ( cm )
AD = 8,1 ( cm )
Diện tích tam giác AMD là :
2,7 x 8,1 : 2 = 10,935 ( cm2 )
NC = 8,1 : 3 x 2 = 5,4 ( cm )
DC = 8,1 ( cm )
Diện tích tam giác DCN là :
8,1 x 5,4 : 2 = 21,87 ( cm2 )
SDMN=SABCD - SBMN - SAMD - SDCN
=> Diện tích hình tam giác DMN là :
65,61 - 7,29 - 10,935 - 21,87 = 25,515 ( cm2 )
b) Dễ thấy MN song song với AC nên MN sẽ vuông góc với BD
Xét tam giác MEB = tam giác NEB ( cạnh huyền cạnh góc vuông)
=> EM=EN
Đúng 0
Bình luận (0)

giúp e vs ạ e đang cần gấp e xin mng e cần gấp nên mng làm giúp e vs
g: \(=\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\)
h: \(=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}\)
\(=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
Đúng 0
Bình luận (0)
\(e,=\dfrac{1}{x-1}-\dfrac{2x}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x^2-2x+1}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{\left(x-1\right)^2}{\left(x^2+1\right)\left(x-1\right)}=\dfrac{x-1}{x^2+1}\\ f,=\dfrac{3x-1}{2\left(3x+1\right)}+\dfrac{3x+1}{2\left(3x-1\right)}-\dfrac{6x}{\left(3x-1\right)\left(3x+1\right)}\\ =\dfrac{9x^2-6x+1+9x^2+6x+1-12x}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{2\left(3x-1\right)^2}{2\left(3x-1\right)\left(3x+1\right)}=\dfrac{3x-1}{3x+1}\)
\(g,=\dfrac{x}{x\left(x-2\right)}-\dfrac{x^2+4x}{x\left(x-2\right)\left(x+2\right)}-\dfrac{2}{x\left(x+2\right)}\\ =\dfrac{x^2+2x-x^2-4x-2x+4}{x\left(x-2\right)\left(x+2\right)}=\dfrac{-4x+4}{x\left(x-2\right)\left(x+2\right)}\\ h,=\dfrac{2x^2+1-x^2+1-x^2+x-1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{x+1}{\left(x+1\right)\left(x^2-x+1\right)}=\dfrac{1}{x^2-x+1}\)
Đúng 0
Bình luận (0)
Coá ai ko giúp em bài này với ạ. Em đang cần gấp trước 1h00 . Em xin cảm ơn