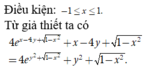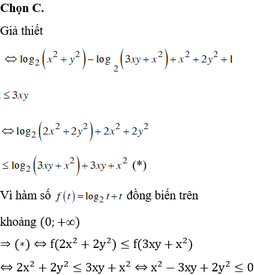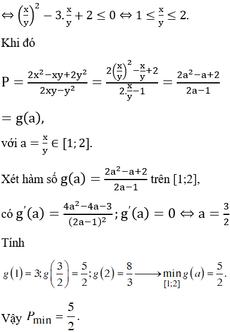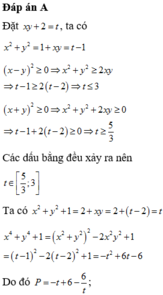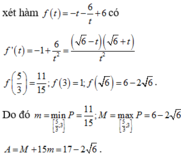Cho các số thực x,y,z thỏa mãn x4 + y4 + x2 - 3= 2y2(1-x2)
Tìm GTLN của x2 + y2

Những câu hỏi liên quan
bài 1: cho các số dương x, y, z thỏa mãn x+y+z=1. Tìm min
a) A = x2+y2+z2
b) B = x2+y2+3z2
c) C=x2+2y2+3z2
d) D=x2+by2+cz2
Cho x,y,z là các số thực thỏa mãn:
-2≤x,y,z≤5 và x+2y+3z≤9. Tìm GTLN của bt:
M= x2 +2y2 +3z2
Cho 2 hai số thực x, y thỏa mãn
e
x
-
4
y
+
1
-
x
2
-
e
y
2
+
1
-
x...
Đọc tiếp
Cho 2 hai số thực x, y thỏa mãn e x - 4 y + 1 - x 2 - e y 2 + 1 - x 2 - y = y 2 - x 4 . Giá trị lớn nhất của biểu thức P = x 3 + 2 y 2 - 2 x 2 + 8 y - x + 2 bằng
A. 2
B. 58 27
C. 115 27
D. 122 27
1. Cho x,y thỏa mãn: x2 + 5y2 - 4xy + 2y = 3. Tìm x,y sao cho x đạt GTLN
2. Cho x,y thỏa mãn: 3x2 + y2 + 2xy + 4 = 7x + 3y
a) Tìm GTNN, GTLN của biểu thức P = x + y
b) Tìm GTNN, GTLN của x
3. Cho x,y thỏa mãn: x2 + 2y2 + 2xy + 7x + 7y + 10 = 0. Tìm GTLN, GTNN của S = x + y
Các số thực a,b,c,x,y,z thỏa mãn
a
2
+
b
2
+
c
2
-
2
a
+
4
c
+
4
0
và
x
2
+
y
2
+
z
2
-
4
x
+
4
y
+
4...
Đọc tiếp
Các số thực a,b,c,x,y,z thỏa mãn a 2 + b 2 + c 2 - 2 a + 4 c + 4 = 0 và x 2 + y 2 + z 2 - 4 x + 4 y + 4 = 0 . Tìm GTLN của S = a - x 2 + b - y 2 + z - c 2 .
![]()
![]()
![]()
![]()
cho x y z là các số thực dương thỏa mãn x + y + z = 3.Tìm GTLN của A= xy/căn(z2+3) + yz/căn(x2+3) + zx/căn(y2+3)
Cho các số thực x, y dương và thỏa mãn
log
2
x
2
+
y
2
3
xy
+
x
2
+
2
log
2
x
2
+...
Đọc tiếp
Cho các số thực x, y dương và thỏa mãn log 2 x 2 + y 2 3 xy + x 2 + 2 log 2 x 2 + 2 y 2 + 1 ≤ log 2 8 xy .Tìm giá trị nhỏ nhất của biểu thức P = 2 x 2 - xy + 2 y 2 2 xy - y 2 .
1.Cho các số thực x, y thỏa mãn x+y+4=0. Tìm GTLN của biểu thức: A= 2(x3+y3)+3(x2+y2)+10xy
Cho x, y là những số thực thỏa mãn
x
2
–
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x...
Đọc tiếp
Cho x, y là những số thực thỏa mãn x 2 – x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15 m là
A. A = 17 - 2 6
B. A = 17 - 6
C. A = 17 + 6
D. A = 17 + 2 6
Cho x,y là những số thực thỏa mãn
x
2
-
x
y
+
y
2
1
. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của
P
x
4
+
y
4
+
1
x
2
+
y...
Đọc tiếp
Cho x,y là những số thực thỏa mãn x 2 - x y + y 2 = 1 . Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của P = x 4 + y 4 + 1 x 2 + y 2 + 1 . Giá trị của A = M + 15m là
A. A = 17 - 2 6
B. A = 17 + 6
C. A = 17 + 2 6
D. A = 17 - 6