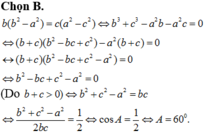Cho tam giác ABC cân tại C có góc C= 360 và AB=a, AC=BC= c. CMR: a2-c2=ac

Những câu hỏi liên quan
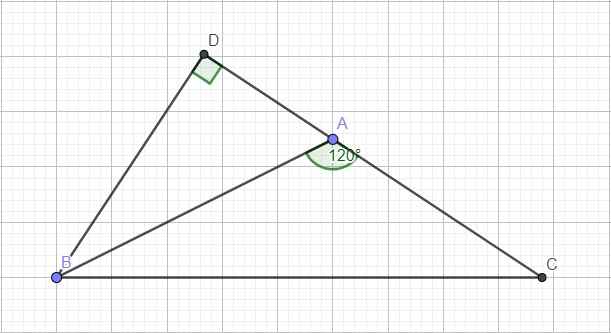
Cho tam giác ABC có góc A = 120 độ, BC = a, AC = b, AB = c. Chứng minh rằng a2 = b2 + c2 + bc ?
Kẻ đường cao BD ứng với AC. Do góc A tù \(\Rightarrow\) D nằm ngoài đoạn thẳng AC hay \(CD=AD+AC\) và \(\widehat{DAB}=180^0-120^0=60^0\)
Áp dụng định lý Pitago:
\(AB^2=BD^2+AD^2\) \(\Rightarrow BD^2=AB^2-AD^2\)
Trong tam giác vuông ABD:
\(cos\widehat{BAD}=\dfrac{AD}{AB}\Rightarrow\dfrac{AD}{AB}=cos60^0=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}AB\)
\(\Rightarrow BD^2=AB^2-\left(\dfrac{1}{2}AB^2\right)=\dfrac{3}{4}AB^2\)
Pitago tam giác BCD:
\(BC^2=BD^2+CD^2=\dfrac{3}{4}AB^2+\left(AD+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\left(\dfrac{1}{2}AB+AC\right)^2\)
\(=\dfrac{3}{4}AB^2+\dfrac{1}{4}AB^2+AB.AC+AC^2\)
\(=AB^2+AB.AC+AC^2\)
Hay \(a^2=b^2+c^2+bc\)
Đúng 3
Bình luận (0)
cho tam giác ABC, góc A=120 độ, AB=c, BC=a, AC=b. C/m: a2=b2+c2+bc
cho tam giac abc vuông tại a, AB 3cm bc 5 cm so sánh góc b và c
Cho tam giác ABC có AB=6cm, AC=8cm, tia phân giác góc A cắt BC tại D. CMR: góc ADB<góc ADC.
Cho tam giác ABC cân tại A có chu vi = 20cm.Cạnh y của BC=6cm. So sánh các góc của ABC?
Bài 1:
AC=4cm
Xét ΔABC có AB<AC
nên \(\widehat{C}< \widehat{B}\)
Bài 2:
BC=6cm
=>AB+AC=14cm
mà AB=AC
nên AB=AC=7cm
Xét ΔABC có AB=AC>BC
nên \(\widehat{B}=\widehat{C}>\widehat{A}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB=a, AC=b, AB=c. Biết b(b2- a2)=c(a2 -c2). Số đo của góc A bằng
A. 30 °
B. 60 °
C. 150 °
D. 120 °
cho tam giác abc cân tại a có bc = 6cm đg cao ah =4cm h thuộc bc 2đg trung trực của ab và ac cắt nhau tại o
a) tính ab ,ac so sánh các góc trong tam giác abc
b)cm 3đ a,o,h thẳng hàng và oa=ob=oc
c)cmr om =on
Cho tam giác ABC cân tại A và M là trung điểm BC. CMR:
a) Tam giác ABM = Tam giác ACM
b) Từ M vẽ MH vuông góc với AB, MK vuông góc với AC. CMR: BH = CK
c) Từ B kẻ BP vuông góc với AC, BP cắt MH tại I. CMR: tam giác IBM cân
B. Phần Hình họcBài 1 (14/56): Cho tam giác ABC vuông tại A, có AB 6cm; AC 8cm.a) Tính BC.b) Kẻ AH vuông góc với BC, biết AH 4,8cm. Tính BH và CH?Bài 2 (55/57): Cho tam giác ABC vuông cân tại A, biết AB AC 4cm.a) Tính BC.b) Kẻ AD vuông góc với BC. CMR: D là trung điểm của BC.c) Từ D kẻ DE vuông góc với AC. CMR: Tam giác AED vuông cân.d) Tính AD.Bài 3 (64/63): Cho đoạn thẳng AB và điểm C nằm giữa A và B. Trên cùng một nửa mặtphẳng bờ AB vẽ hai tam giác đều ACD và BCE. Gọi M, N lần lượt là tr...
Đọc tiếp
B. Phần Hình học
Bài 1 (14/56): Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm.
a) Tính BC.
b) Kẻ AH vuông góc với BC, biết AH = 4,8cm. Tính BH và CH?
Bài 2 (55/57): Cho tam giác ABC vuông cân tại A, biết AB = AC = 4cm.
a) Tính BC.
b) Kẻ AD vuông góc với BC. CMR: D là trung điểm của BC.
c) Từ D kẻ DE vuông góc với AC. CMR: Tam giác AED vuông cân.
d) Tính AD.
Bài 3 (64/63): Cho đoạn thẳng AB và điểm C nằm giữa A và B. Trên cùng một nửa mặt
phẳng bờ AB vẽ hai tam giác đều ACD và BCE. Gọi M, N lần lượt là trung điểm của AE
và BD. CMR:
a) AE = BD.
b)
= CME CNB .
c) Tam giác MNC là tam giác đều.
B. Phần Hình họcBài 1 (14/56): Cho tam giác ABC vuông tại A, có AB 6cm; AC 8cm.a) Tính BC.b) Kẻ AH vuông góc với BC, biết AH 4,8cm. Tính BH và CH?Bài 2 (55/57): Cho tam giác ABC vuông cân tại A, biết AB AC 4cm.a) Tính BC.b) Kẻ AD vuông góc với BC. CMR: D là trung điểm của BC.c) Từ D kẻ DE vuông góc với AC. CMR: Tam giác AED vuông cân.d) Tính AD.Bài 3 (64/63): Cho đoạn thẳng AB và điểm C nằm giữa A và B. Trên cùng một nửa mặtphẳng bờ AB vẽ hai tam giác đều ACD và BCE. Gọi M, N lần lượt là tr...
Đọc tiếp
B. Phần Hình học
Bài 1 (14/56): Cho tam giác ABC vuông tại A, có AB = 6cm; AC = 8cm.
a) Tính BC.
b) Kẻ AH vuông góc với BC, biết AH = 4,8cm. Tính BH và CH?
Bài 2 (55/57): Cho tam giác ABC vuông cân tại A, biết AB = AC = 4cm.
a) Tính BC.
b) Kẻ AD vuông góc với BC. CMR: D là trung điểm của BC.
c) Từ D kẻ DE vuông góc với AC. CMR: Tam giác AED vuông cân.
d) Tính AD.
Bài 3 (64/63): Cho đoạn thẳng AB và điểm C nằm giữa A và B. Trên cùng một nửa mặt
phẳng bờ AB vẽ hai tam giác đều ACD và BCE. Gọi M, N lần lượt là trung điểm của AE
và BD. CMR:
a) AE = BD.
b)
= CME CNB .
c) Tam giác MNC là tam giác đều.
Bài 1
a. (Tự vẽ hình)
Áp dụng định lí Py-ta-go, ta có:
BC2= AB2 + AC2
<=> BC2= 62 + 82
<=> BC2= 100
=> BC = 10 (cm)
Bài 1
b. Áp dụng định lí Py-ta-go, ta có:
AC2 = AH2 + HC2
<=> 82 = 4,82 + HC2
<=> 64 = 23,04 + HC2
=> HC2 = 64 - 23,04
=> HC2 = 40,96
=> HC = 6,4 (cm)
=> HB = BC - HC = 10 - 6,4 = 3,6 (cm)
Cho tam giác ABC vuông góc tại A và AB bé hơn AC. Trên tia đối của tia AB lấy điểm E sao cho AEABa So sánh góc B và góc C của tam giác ABC, tính BC khi AB6cmb C/m tam giác BCE cân và CA là tia phân giác của góc BCEc Gọi K là trung điểm của CE, BK cắt AC tại G; Từ K kẻ đường song song với BE, cắt AC tại I và cắt BC tại M. Cmr M là trung điểm của BCd Tam giác ABC cần thêm điều kiện gì để GAGMGK
Đọc tiếp
Cho tam giác ABC vuông góc tại A và AB bé hơn AC. Trên tia đối của tia AB lấy điểm E sao cho AE=AB
a So sánh góc B và góc C của tam giác ABC, tính BC khi AB=6cm
b C/m tam giác BCE cân và CA là tia phân giác của góc BCE
c Gọi K là trung điểm của CE, BK cắt AC tại G; Từ K kẻ đường song song với BE, cắt AC tại I và cắt BC tại M. Cmr M là trung điểm của BC
d Tam giác ABC cần thêm điều kiện gì để GA=GM=GK