Biểu diễn miền nghiệm của bpt 2x-y<3

Những câu hỏi liên quan
Biểu diễn miễn nghiệm của hệ phương trình:-2x+y=2; -x+2y=4; x+y=5 giải thích và vẽ miền nghiệm
Trong các khẳng định sau, khẳng định nào đúng?A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2. B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trìnhvà (x; y) (-1; 1) là một nghiệm của hệ. C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và (x; y) (-2; 1) là một nghiệm của hệ. D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình và...
Đọc tiếp
Trong các khẳng định sau, khẳng định nào đúng?
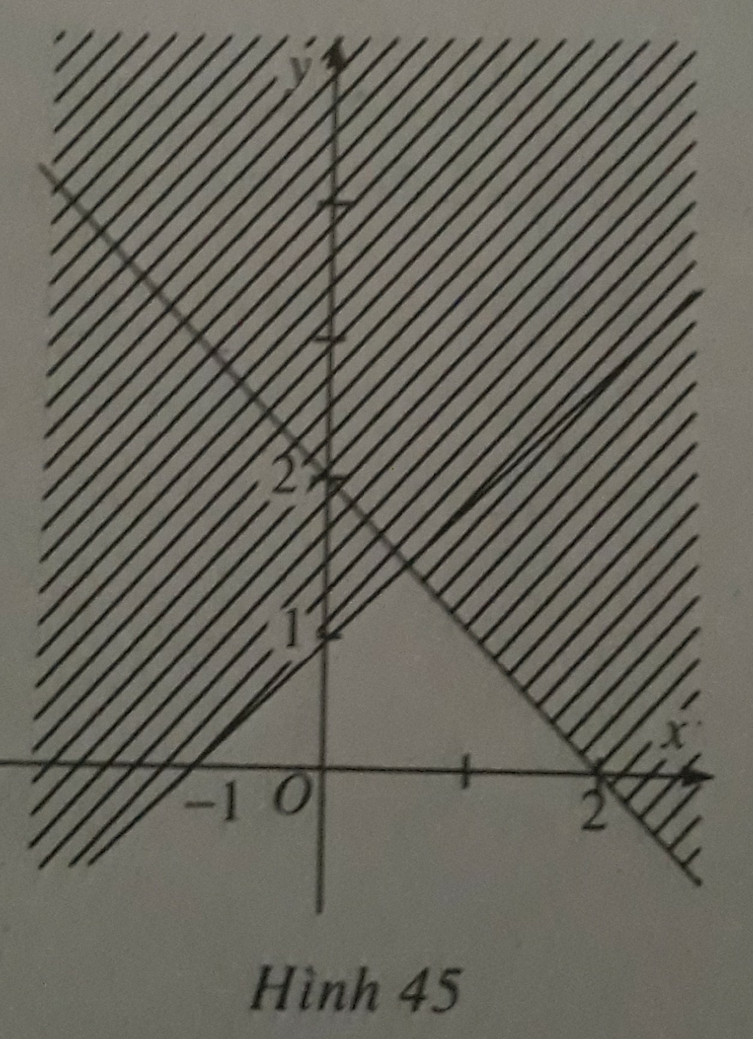
A. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình x + y ≤ 2.
B. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình![]()
và (x; y) = (-1; 1) là một nghiệm của hệ.
C. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình ![]() và (x; y) = (-2; 1) là một nghiệm của hệ.
và (x; y) = (-2; 1) là một nghiệm của hệ.
D. Hình 45 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình 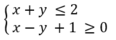 và (x; y) = (1; 0) là một nghiệm của hệ.
và (x; y) = (1; 0) là một nghiệm của hệ.
Biểu diễn miền nghiệm của bất phương trình:
a) \(3x - y > 3\)
b) \(x + 2y \le - 4\)
c) \(y \ge 2x - 5\)
a) \(3x - y > 3\)
Bước 1: Vẽ đường thẳng \(d: 3x - y = 3 \Leftrightarrow y = 3x - 3\) đi qua A(0;-3) và B(1;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(3x - y > 3 \Leftrightarrow 3.0 - 0 > 3\)(Vô lí)
=> O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, không chứa điểm O.
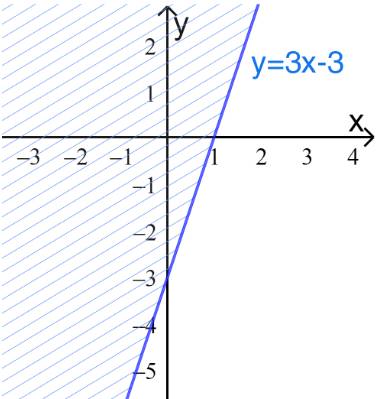
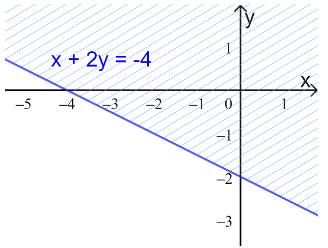
b) \(x + 2y \le - 4\)
Bước 1: Vẽ đường thẳng \(d: x + 2y = - 4 \Leftrightarrow y = - \frac{1}{2}x - 2\) đi qua A(0;-2) và B(-4;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(x + 2y \le - 4 \Leftrightarrow 0 + 2.0 \le - 4\)(Vô lí)
=> O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, không chứa điểm O.
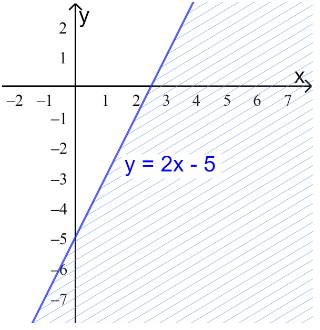
c) \(y \ge 2x - 5\)
Bước 1: Vẽ đường thẳng \(y = 2x - 5\) đi qua A(0;-5) và B(2.5;0)
Bước 2: Thay tọa độ O(0;0) vào bất phương trình ta được:
\(y \ge 2x - 5 \Leftrightarrow 0 \ge 2.0 - 5\)(Luôn đúng)
=> O thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm là nửa mp bờ d, chứa điểm O.
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của các bất phương trình sau:
a) \(2x + y - 2 \le 0\)
b) \(x - y - 2 \ge 0\)
Tham khảo:
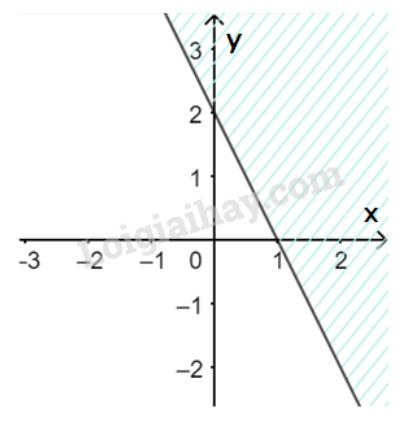
a) Vẽ đường thẳng \(\Delta :2x + y - 2 = 0\) đi qua hai điểm \(A(0;2)\) và \(B\left( {1;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(2.0 + 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), chứa gốc tọa độ O
(miền không gạch chéo trên hình)
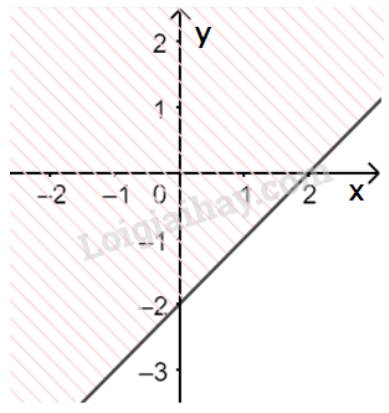
b) Vẽ đường thẳng \(\Delta :x - y - 2 = 0\) đi qua hai điểm \(A(0; - 2)\) và \(B\left( {2;0} \right)\)
Xét gốc tọa độ \(O(0;0).\) Ta thấy \(O \notin \Delta \) và \(0 - 0 - 2 = - 2 < 0\)
Do đó, miền nghiệm của bất phương trình là nửa mặt phẳng kể cả bờ \(\Delta \), không chứa gốc tọa độ O
(miền không gạch chéo trên hình)
Đúng 0
Bình luận (0)
Hình 43 (miền không bị gạch, kể cả biên) biểu diễn miền nghiệm của bất phương trình nào sau đây?
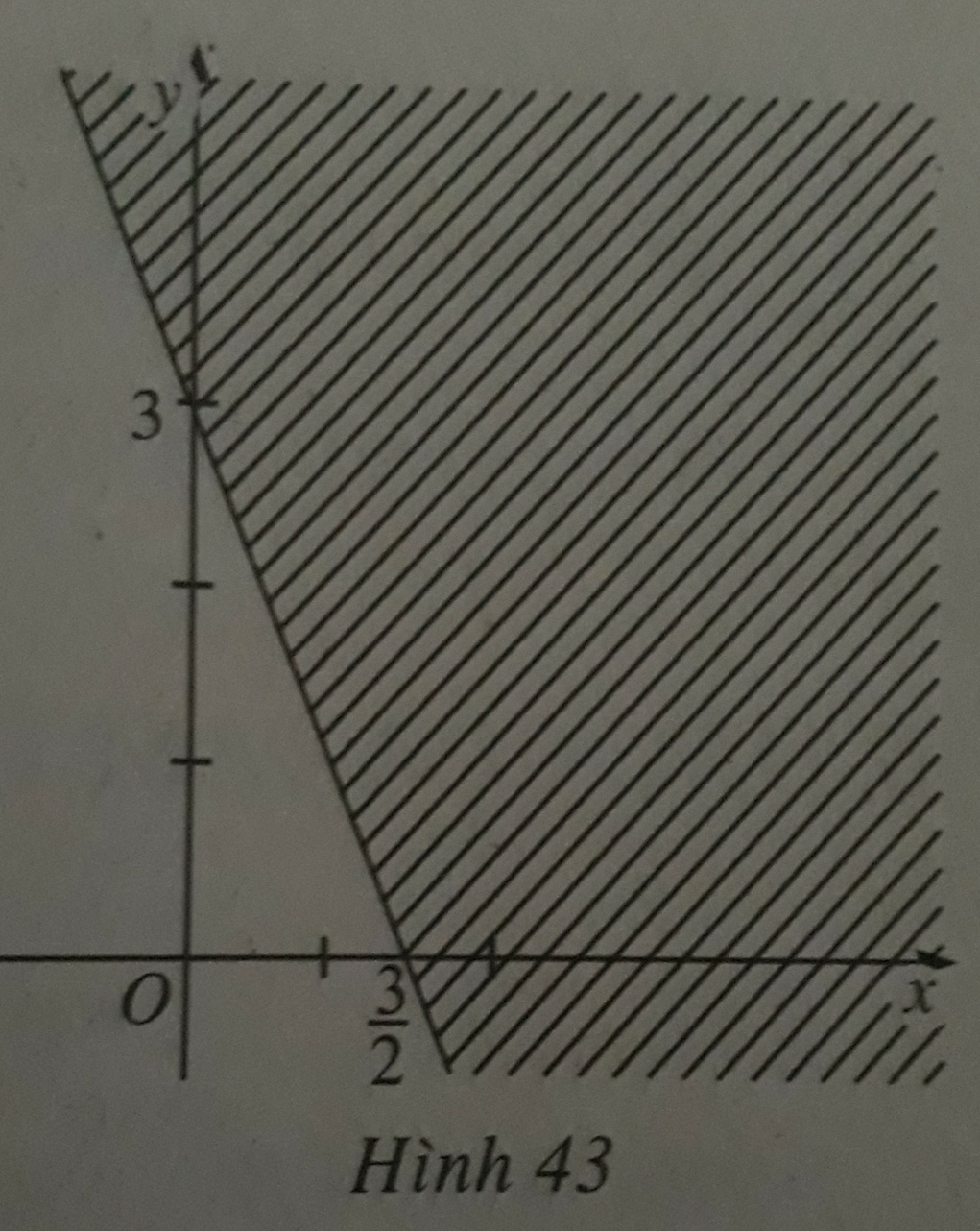
A. x + 2y > 3
B. 2x + y ≤ 3
C. 2x + y < 3
D. x + y - 3 ≤ 0
Biểu diễn miền nghiệm của hệ bất phương trình sau: \(\left\{ \begin{array}{l}3x - y > - 3\\ - 2x + 3y < 6\\2x + y > - 4\end{array} \right.\)
Vẽ đường thẳng \(3x - y = - 3\) (nét đứt)
Thay tọa độ O vào \(3x - y > - 3\) ta được \(3.0 - 0 > - 3\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \( - 2x + 3y = 6\) (nét đứt)
Thay tọa độ O vào \( - 2x + 3y < 6\) ta được \( - 2.0 + 3.0 < 6\) (Đúng)
Gạch đi phần không chứa O
Vẽ đường thẳng \(2x + y = - 4\)(nét đứt)
Thay tọa độ O vào \(2x + y > - 4\) ta được \(2.0 + 0 > - 4\) (Đúng)
Gạch đi phần không chứa O
Miền nghiệm của hệ là phần không bị gạch chéo:
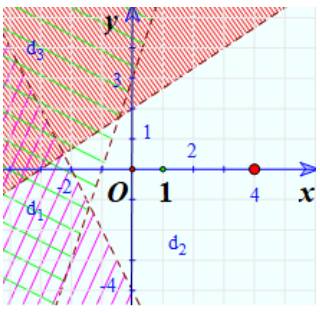
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của bất phương trình 2x + y < 200.
Tham khảo:
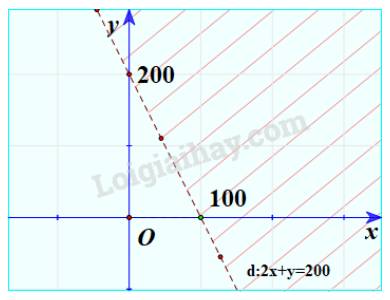
Ta biểu diễn miền nghiệm của bất phương trình bậc nhất hai ẩn 2x+y<200
Bước 1: Vẽ đường thẳng d: 2x+y=200 trên mặt phẳng tọa độ Oxy.
Bước 2: Lấy một điểm bất kì không thuộc d trên mặt phẳng rồi thay vào biểu thức 2x+y. Chẳng hạn, lấy O(0;0), ta có: 2.0+0<200
Do đó miền nghiệm của bất phương trình đã cho là nửa mặt phẳng bờ d chứa gốc tọa độ không kể đường thẳng d. (miền không bị gạch).
Chú ý
Miền nghiệm của bất phương trình 2x+y
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của mỗi bất phương trình sau:
a) \(x + 2y < 3\);
b) \(3x - 4y \ge - 3\);
c) \(y \ge - 2x + 4\);
d) \(y < 1 - 2x\).
Tham khảo:
a) Ta vẽ đường thẳng d’:\(x + 2y = 3 \Leftrightarrow y = - \frac{x}{2} + \frac{3}{2}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(x + 2y < 3\) ta được:
\(0 + 2.0 = 0 < 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
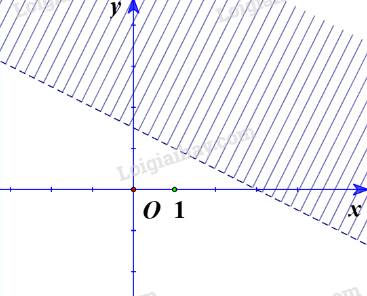
b) Ta vẽ đường thẳng d:\(3x - 4y = - 3 \Leftrightarrow y = \frac{{3x}}{4} + \frac{3}{4}\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(3x - 4y \ge - 3\) ta được:
\(3.0 - 4.0 = 0 \ge - 3\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
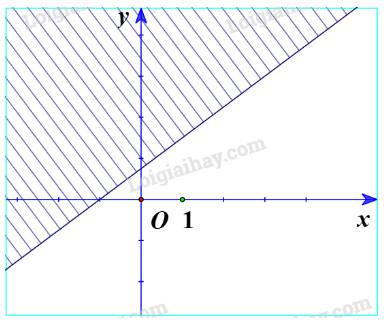
c) Ta vẽ đường thẳng d:\(y = - 2x + 4\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y \ge - 2x + 4\) ta được:
\(0 \ge - 2.0 + 4 \Leftrightarrow 0 \ge 4\) (Vô lí)
Vậy O không nằm trong miền nghiệm.
Ta có miền nghiệm:
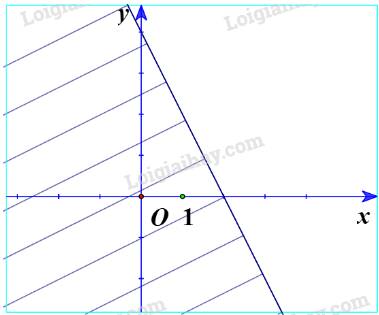
d) Ta vẽ đường thẳng d:\(y = 1 - 2x\)
Thay tọa độ điểm O(0;0) vào bất phương trình \(y < 1 - 2x\) ta được:
\(0 < 1 - 2.0\) (Luôn đúng)
Vậy O nằm trong miền nghiệm.
Ta có miền nghiệm:
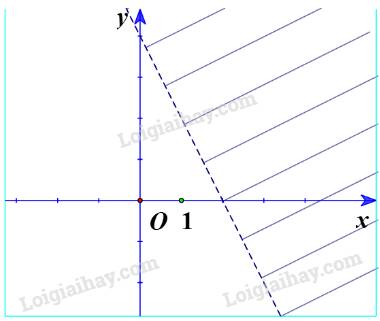
Chú ý
Đối với các bất phương trình có dấu “<” hoặc “>” thì vẽ đường thẳng là nét đứt.
Đối với các bất phương trình có dấu “\( \le \)” hoặc “\( \ge \)” thì vẽ đường thẳng là nét liền.
Đúng 0
Bình luận (0)
Biểu diễn miền nghiệm của bất phương trình \(\dfrac{{x + y}}{2} \ge \dfrac{{2x - y + 1}}{3}\) trên mặt phẳng tọa độ.
\(\begin{array}{l}\dfrac{{x + y}}{2} \ge \dfrac{{2x - y + 1}}{3}\\ \Leftrightarrow 3\left( {x + y} \right) \ge 2\left( {2x - y + 1} \right)\\ \Leftrightarrow 3x + 3y \ge 4x - 2y + 2\\ \Leftrightarrow x - 5y \le - 2\end{array}\)
Biểu diễn miền nghiệm của bất phương trình:
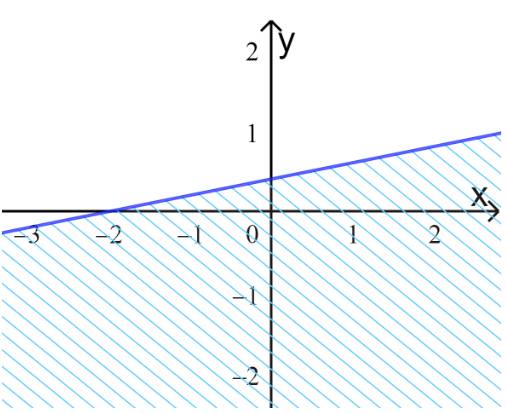
Bước 1: Vẽ đường thẳng d:\(x - 5y = - 2\) (nét liền) đi qua A(-2;0) và B(0;0,4)
Bước 2: Lấy tọa độ điểm O(0;0) thay vào biểu thức x-5y ta được: x-5y=0-5.0=0>-2
=> Điểm O không thuộc miền nghiệm của bất phương trình.
Vậy miền nghiệm của BPT đã cho là nửa mặt phẳng có bờ là đường thẳng d:\(x - 5y = - 2\) và không chứa gốc tọa độ O.
Đúng 1
Bình luận (0)
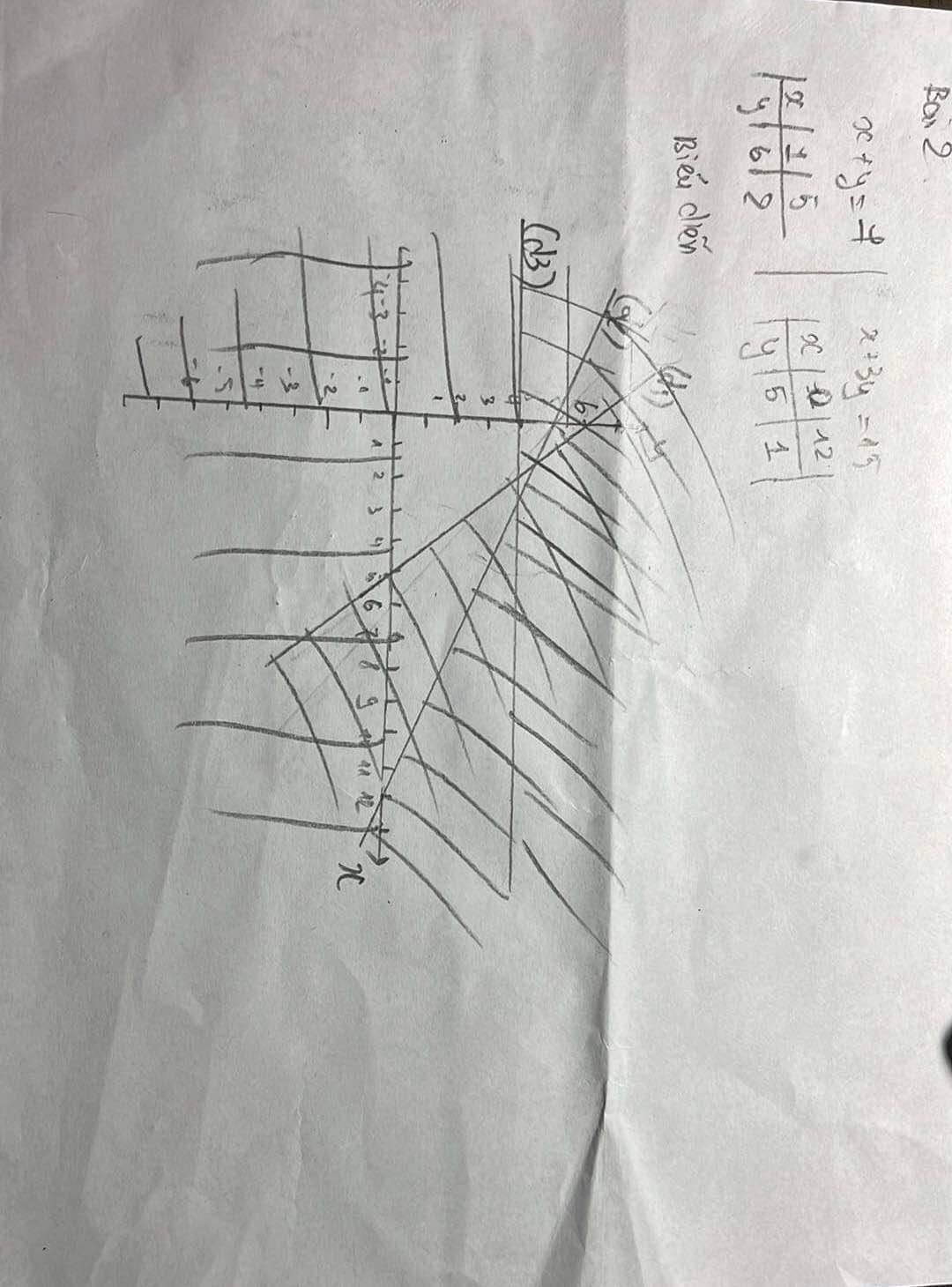
Bài 2 (1 điểm)
a) Biểu diễn miền nghiệm của hệ bpt $left{ begin{aligned} & xge 0 & 0le yle 4 & x+yle 7 & x+3yle 15 end{aligned} right.$.
b) Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một sản phẩm loại I cần dùng $1$ máy nhóm A và $1$ máy nhóm B. Để sản xuất ra một sản phẩm loại $2$ cần dùng $1$ máy nhóm A, $3$ máy nhóm B và $2$ máy nhóm C. Nhà máy có $7$ máy nhóm A, $15$ máy nhóm B, $8$ máy nhóm C. Biết một sản phẩm loại I lãi $10$ nghìn đồng, một sản...
Đọc tiếp
Bài 2 (1 điểm)
a) Biểu diễn miền nghiệm của hệ bpt $\left\{ \begin{aligned} & x\ge 0 \\ & 0\le y\le 4 \\ & x+y\le 7 \\ & x+3y\le 15 \\ \end{aligned} \right.$.
b) Có ba nhóm máy A, B, C dùng để sản xuất ra hai loại sản phẩm I và II. Để sản xuất một sản phẩm loại I cần dùng $1$ máy nhóm A và $1$ máy nhóm B. Để sản xuất ra một sản phẩm loại $2$ cần dùng $1$ máy nhóm A, $3$ máy nhóm B và $2$ máy nhóm C. Nhà máy có $7$ máy nhóm A, $15$ máy nhóm B, $8$ máy nhóm C. Biết một sản phẩm loại I lãi $10$ nghìn đồng, một sản phẩm loại II lãi $15$ nghìn đồng. Hãy lập phương án để việc sản xuất hai loại sản phẩm trên có lãi là cao nhất.