 Chứng minh hằng đẳng thức
Chứng minh hằng đẳng thức

Những câu hỏi liên quan
Từ định nghĩa của sinα, cosα. Hãy chứng minh hằng đẳng thức đầu tiên, từ đó suy ra các hằng đẳng thức còn lại.
cosα = OH¯; sinα = OK¯
Do tam giác OMK vuông tại K nên:
sin2 α + cos2 α = OK¯2 + OH¯2 = OK2 + MK2 = OM2 = 1.
Vậy sin2 α + cos2 α = 1.
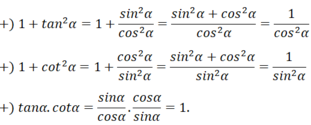
Đúng 0
Bình luận (0)
là chứng minh hằng đẳng thức
CM HĐT là
VD CM
( x + y)^2 = x^2 + 2xy + y^2
Phải không bạn
Đúng 0
Bình luận (0)
chứng minh hằng đẳng thức: (x+a)(x+b)=x^2+(a+b)x+ab
\(\left(x+a\right)\left(x+b\right)\)
=>\(x^2+bx+ax+ab\)
=>\(x^2+\left(a+b\right)x+ab\)(ĐPCM)
Nhớ H cho mik nhé, các bạn.
Đúng 0
Bình luận (0)
Chứng minh hằng đẳng thức: a + b + c 3 = a 3 + b 3 + c 3 + 3(a+b)(b+c)(c+a)
Biến đổi vế trái:
a + b + c 3 = a + + c 3 = a + b 3 +3 a + b 2 c+3(a+b) c 2 + c 3
= a 3 + 3 a 2 b + 3a b 2 + b 3 + 3( a 2 + 2ab + b 2 )c + 3a c 2 + 3b c 2 + c 3
= a 3 + 3 a 2 b + 3a b 2 + b 3 + 3 a 2 c + 6abc + 3 b 2 c + 3a c 2 + 3b c 2 + c3
= a 3 + b 3 + c 3 + 3 a 2 b + 3a b 2 + 3 a 2 c + 6abc + 3 b 2 c + 3a c 2 + 3b c 2
= a 3 + b 3 + c 3 + (3 a 2 b + 3a b 2 ) +( 3 a 2 c + 3abc)+ (3abc + 3 b 2 c)+(3a c 2 + 3b c 2 )
= a 3 + b 3 + c 3 + 3ab(a + b) + 3ac(a + b) + 3bc(a + b) + 3 c 2 (a + b)
= a 3 + b 3 + c 3 + 3(a + b)(ab + ac + bc + c 2 )
= a 3 + b 3 + c 3 + 3(a + b)[a(b + c) + c(b + c)]
= a 3 + b 3 + c 3 + 3(a + b)(b + c)(a + c) (đpcm)
Đúng 0
Bình luận (0)
Chứng minh đa thức vô nghiệm
X2+x+1/2 (chứng minh cách lớp 7, ko dùng hằng đẳng thức)
\(x^2+x+\frac{1}{2}\)
\(=x^2+2.x.\frac{1}{2}+\frac{1}{4}-\frac{1}{4}+\frac{1}{2}\)
\(=\left(x+\frac{1}{2}\right)^2+\frac{1}{4}\ge\frac{1}{4}>;0\forall x\)
Vậy đa thức trên vô nghiệm
Đúng 0
Bình luận (0)
Chứng minh hằng đẳng thức: -a.(b-c)-b.(c-a)=-c.(b-c)
vế tra= -ab+ac-bc+ab=ac-bc=-c(b-c)
Các bạn giúp mình nha :))
Ta có : -a . ( b - c ) - b . ( c -a )
= -ab + ac - bc + ab
= ac - bc
= c. ( a- b )
Mà c . ( a- b ) = c . ( a - b )=> -a . ( b - c ) - b . ( c - a ) = -c . ( b -c ) => đpcm
Chứng minh hằng đẳng thức sau
a) a^2+b^2= (a+b) ^2-2ab
\(a^2+b^2\) = (a+b)\(^2\) - 2ab
ta có
(a+b)\(^2\) - 2ab
= a\(^2\) + 2ab + b\(^2\) - 2ab
= a\(^2\) + b\(^2\) ( đpcm)
Đúng 0
Bình luận (0)
Dùng hằng đẳng thức đề chứng minh: x - x^2 -1 <0 với mọi số thực x
Đặt \(A=x-x^2-1\)\(\Rightarrow2A=2x-2x^2-2=-\left(x^2-2x+1\right)-x^2-1=-\left[\left(x-1\right)^2+x^2\right]-1< 0\)
\(\Rightarrow2A< 0\Rightarrow A< 0\)
Đúng 0
Bình luận (0)
Cho K(x)= x^8-x^5+x^2-x+1 Chứng minh K(x) ko có nghiệm bằng hằng đẳng thức
Xem chi tiết
`K(x)=x^8-x^5+x^2-x+1=x^2(x^6-x^3+1/4)+(3/4x^2-x+1)=x^2(x^3-1/2)^2+3/4(x-2/3)^2+2/3>0AAx`
Vậy `K(x)` vô nghiệm
Đúng 0
Bình luận (0)
chứng minh các hằng đẳng thức sau:(a-b)^3=-(b-a)^3
(-a-b)^2=(a+b)^2




















