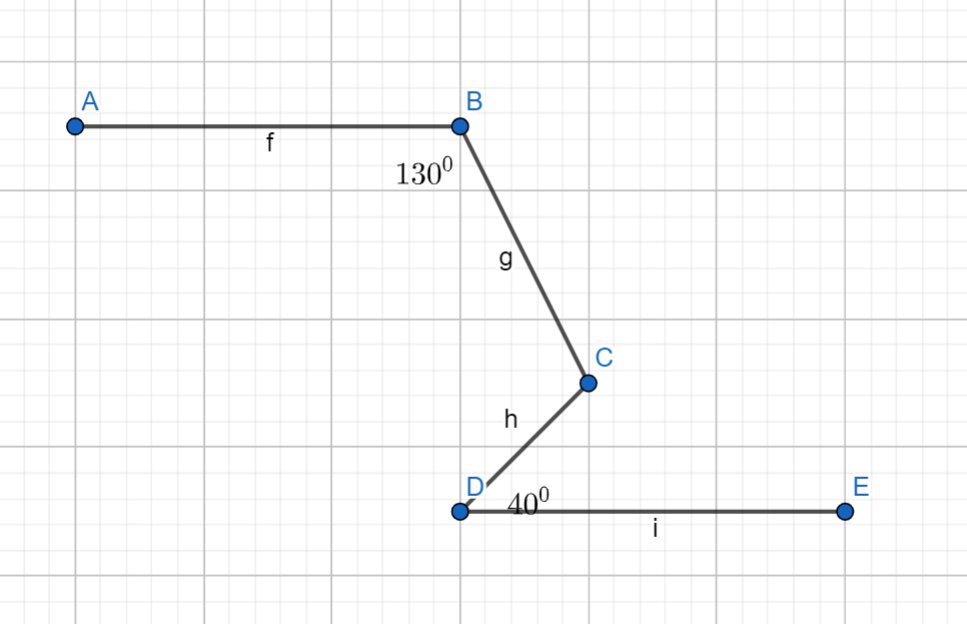
Cho AB//DE
Tính góc ACD
Cho hình vẽ, biết AB//DE và góc BAC= 120 độ; góc ACD= 130 độ. Tính góc DAC+ ACD+CDE?
cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90
Cho tam giác ABC. Trên tia đối của AB lấy điểm D sao cho AC = AD
Khi đó AB + AC = AB + AD = BD, còn ACD là tam giác cân, nên góc ACD = góc ADC, tức là góc BDC = góc ACD
Mặt khác, do tia CA nằm giữa CB và CD nên góc BCD > góc DCA
Khi đó, trong tam giác BCD có: góc BCD > góc BDC nên BD > BC hay AB + AC > BC
Tương tự, em hãy chứng minh, trong tam giác ABC có: CA + CB > AB và BA + BC > CA
Cho hình thang ABCD (AB//CD). Cm góc ACD= góc BDC
- Gọi O là giao điểm của AC và BD.
- AB//CD nên góc BAC = góc ACD (so le trong), tương tự góc ABD=góc BDC.
- Theo đề bài góc ACD=góc BDC nên góc BAC=góc ABD.
=>Tam giác ABO cân tại O => 0A=0B.(1)
Tương tự tam giác ODC cân tại O =>OD=OC.(2)
Lại có góc AOD=góc BOC (đối đỉnh ) (3)
Từ (1), (2), (3) suy ra tam giác AOD = tam giác OBC nên suy ra :
- AD=BC
- Góc ADB=góc BCA
suy ra hình thang ABCD cân(hình thang có hai cạnh bên bằng nhau và hai góc ở đáy bằng nhau
cho đường tròn tâm o đường kính ab dây cd//ab. cd cùng chiều tia ab. chứng minh: a) góc adc = góc bcd b) góc acd = góc adc =90
cho hình thang cân ABCD(AB//CD). a C/M góc ACD = góc BDC b gọi E là giao điểm của AC và BD . C/M AE=BE Giúp mik vs
a: Xét ΔACD và ΔBDC có
AD=BC
\(\widehat{ADC}=\widehat{BCD}\)
AC chung
Do đó: ΔACD=ΔBDC
Suy ra: \(\widehat{ACD}=\widehat{BDC}\)
b: Ta có: \(\widehat{EAB}=\widehat{ACD}\)
\(\widehat{EBA}=\widehat{BDC}\)
mà \(\widehat{ACD}=\widehat{BDC}\)
nên \(\widehat{EAB}=\widehat{EBA}\)
Xét ΔEAB có \(\widehat{EAB}=\widehat{EBA}\)
nên ΔEAB cân tại E
hay AE=BE
Cho hình vẽ, biết AB//DE
a) chứng minh rằng ACD=BAC+CDE
b)tính góc ACD biết góc ABC=60độ, góc CDE=32 độ
?? C lấy đâu ra vậy bạn ?
Cho hình thang ABCD(AB//CD) có góc ACD=góc BDC.Chứng minh BD2-BC2=AB.CD.
Cho hình thang ABCD(AB//CD) có góc ACD=góc BDC.Chứng minh BD2-BC2=AB.CD
Kẻ 2 đường cao AE, BF
Gọi G là giao điểm 2 đường chéo
\(\widehat{ACD}=\widehat{BDC}\Rightarrow\Delta GCD\) cân tại G \(\Rightarrow GC=GD\) (1)
\(\left\{{}\begin{matrix}\widehat{ACD}=\widehat{BAC}\left(slt\right)\\\widehat{BDC}=\widehat{ABD}\left(slt\right)\\\widehat{ACD}=\widehat{BDC}\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\widehat{BAC}=\widehat{ABD}\) \(\Rightarrow\Delta GAB\) cân tại G \(\Rightarrow GA=GB\) (2)
(1); (2) \(\Rightarrow AC=BD\Rightarrow ABCD\) là hình thang cân
\(\Rightarrow\left\{{}\begin{matrix}AB=EF\\DE=CF\end{matrix}\right.\)
Áp dụng định lý Pitago: \(\left\{{}\begin{matrix}BD^2=DF^2+BF^2\\BC^2=BF^2+CF^2\end{matrix}\right.\)
\(\Rightarrow BD^2-BC^2=DF^2-CF^2=\left(DF+CF\right)\left(DF-CF\right)=CD.EF=CD.AB\) (đpcm)
cho tam giác ABC trên cạnh AB lấy điểm D sao cho AB=BD
Chứng minh tam giác ACD đều
Tính các góc của tam giác ACD