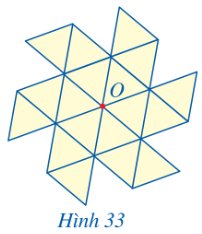
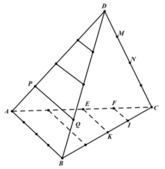
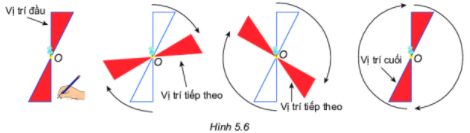
Vẽ trên giấy 18 hình tam giác đều bằng nhau và ở vị trí như Hình 33 (còn gọi là hình chong chóng).
a) Hãy đánh dấu 6 điểm mút của hình chong chóng sao cho 6 điểm mút đó là các đỉnh của một hình lục giác đều tâm O.
b) Hãy chỉ ra những phép quay tâm O giữ nguyên hình chong chóng.