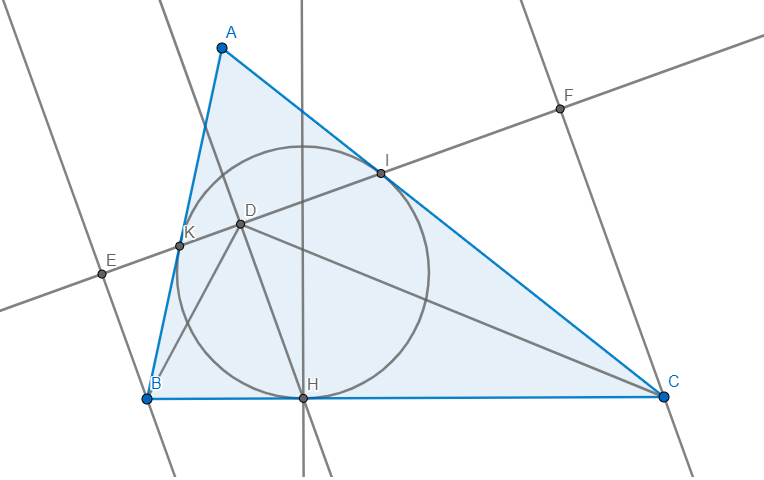
Cho đường tròn (O) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại H, I, K. Vẽ HD vuông góc với IK, chứng minh rằng góc ABD bằng góc ACD.

Những câu hỏi liên quan
Cho đường tròn (O) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại H, I, K. Vẽ HD vuông góc IK. Chứng minh góc ABD = góc ACD.
Cho đường tròn (O) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại H, I, K. Vẽ HD vuông góc IK. Chứng minh góc ABD = góc ACD. Giúp mình nha.
Kẻ \(BE\bot IK,CF\bot IK\)
Vì AK,AI là tiếp tuyến \(\Rightarrow\Delta AKI\) cân tại A \(\Rightarrow\angle AKI=\angle AIK\)
\(\Rightarrow\angle BKE=\angle CIF\)
Xét \(\Delta BEK\) và \(\Delta CFI:\) Ta có: \(\left\{{}\begin{matrix}\angle BKE=\angle CIF\\\angle BEK=\angle CFI=90\end{matrix}\right.\)
\(\Rightarrow\Delta BEK\sim\Delta CFI\left(g-g\right)\Rightarrow\dfrac{BE}{CF}=\dfrac{BK}{CI}\)
Vì BK,BH là tiếp tuyến \(\Rightarrow BH=BK\)
Vì CI,CH là tiếp tuyến \(\Rightarrow CI=CH\)
\(\Rightarrow\dfrac{BK}{CI}=\dfrac{BH}{CH}\Rightarrow\dfrac{BE}{CF}=\dfrac{BH}{CH}\)
Vì \(BE\parallel HD\parallel CF(\bot IK)\) \(\Rightarrow\dfrac{BH}{CH}=\dfrac{ED}{DF}\Rightarrow\dfrac{BE}{CF}=\dfrac{ED}{DF}\)
Xét \(\Delta BED\) và \(\Delta CFD:\) Ta có: \(\left\{{}\begin{matrix}\dfrac{BE}{CF}=\dfrac{DE}{DF}\\\angle BED=\angle CFD=90\end{matrix}\right.\)
\(\Rightarrow\Delta BED\sim\Delta CFD\left(c-g-c\right)\Rightarrow\angle BDE=\angle CDF\)
mà \(\angle AKI=\angle AIK\Rightarrow\angle AKI-\angle BDE=\angle AIK-\angle CDF\)
\(\Rightarrow\angle ABD=\angle ACD\)
Đúng 3
Bình luận (1)
Cho đường tròn (O) nội tiếp tam giác ABC tiếp xúc với các cạnh BC, CA, AB lần lượt tại H, I, K. Vẽ HD vuông góc IK. Chứng minh góc ABD = góc ACD.
Giúp mình nha.
(O) tiếp xúc với BC, CA, AB tại H, I, K \Rightarrow OK vuông với KB ở K.
Mà HD vuông với KD ở D.
∠KBD=∠OKD∠KBD=∠OKD Hay ∠ABD=∠OKI∠ABD=∠OKI
Tương tự có ∠ACD=∠OIK∠ACD=∠OIK
(O) có ΔΔOIK cân ở O \Rightarrow ∠OKI=∠OIK
đó bạn nhé nhớ k nhe
bạn viết lại giùm mình đc ko, chứ mình ko thấy gì hết.
Cho tam giác ABC (AB > AC) ngoại tiếp đường tròn (I) và nội tiếp đường tròn (O). Đường tròn (I) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi H là hình chiếu vuông góc của D trên EF. Đường tròn ngoại tiếp tam giác AEF cắt đường tròn (O) tại K (K khác A)
a) Chứng minh HD là phân giác của góc BHC
b) Chứng minh ba điểm I, H, K thẳng hàng
Xem chi tiết
Cho tam giác ABC không cân. Đường tròn tâm I nội tiếp tam giác , tiếp xúc với các cạnh BC, CA, AB lần lượt tại A', B', C' . Đường thằng B'C' cắt BC tại D. Chứng minh ID vuông góc với AA'
\(\overrightarrow{ID}.\overrightarrow{AA'}=\overrightarrow{ID}\left(\overrightarrow{IA'}-\overrightarrow{IA}\right)=\overrightarrow{ID}.\overrightarrow{IA'}-\overrightarrow{ID}.\overrightarrow{IA}=IA'^2-\overrightarrow{ID}.\overrightarrow{IA}\)
\(=IA'^2-\left(\overrightarrow{IC'}+\overrightarrow{C'D}\right)\overrightarrow{IA}=IA'^2-\overrightarrow{IC'}.\overrightarrow{IA'}-\overrightarrow{C'D}.\overrightarrow{IA}=IA'^2-IC'^2-0\) (vì AI vuông góc với C'B')
\(=r^2-r^2=0\) (r là bán kính đường tròn nội tiếp tam giác ABC)
ĐFCM
Đúng 0
Bình luận (0)
Cho tam giác ABC , AB> AC ngoại tiếp đường tròn (I ) và nội tiếp đường tròn (O). Đường tròn (I ) tiếp xúc với các cạnh BC, CA, AB lần lượt tại D, E, F. Gọi H là hình chiếu vuông góc của D trên EF. Đường tròn ngoại tiếp tam giác AEF cắt đường tròn (O) tại K (K khác A).
a) Chứng minh HD là phân giác của góc BHC .
b) Chứng minh ba điểm I, H, K thẳng hàng.
Cho tam giác ABC nội tiếp đường tròn tâm O và AB<AC . Vẽ AH vuông góc với BC tại H . đường tròn đường kính AH lần lượt cắt AB ,AC tại I và K . Chứng minh ba đường thẳng AD , IK và BC đông qui
giúp em vs
1)Cho tam giác nhọn ABC (ABAC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)2)Cho tam giác ABC (ABAC) nội tiếp đường tròn (O), đường trung tuyến AM. Lấy điểm D trên cung BC không chứa A sao cho góc BAD góc CAM. Chứng minh góc ADB góc CDM3)Cho tam giác ABC nội tiếp đường tròn O tại D. Đường tròn (D;DB) cắt đường thẳng AB tại Q (k...
Đọc tiếp
1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
2)Cho tam giác ABC (AB<AC) nội tiếp đường tròn (O), đường trung tuyến AM. Lấy điểm D trên cung BC không chứa A sao cho góc BAD= góc CAM. Chứng minh góc ADB= góc CDM
3)Cho tam giác ABC nội tiếp đường tròn O tại D. Đường tròn (D;DB) cắt đường thẳng AB tại Q (khác B), cắt đuòng thẳng AC tại P (khác C). Chứng minh rằng AO vuông góc PQ
Các bạn giúp mình nhé để mình làm cho xong bài tập kẻo xuân này con không về
1)Cho tam giác nhọn ABC (AB<AC) nội tiếp đường tròn (O). Gọi H là trực tâm của tam giác ABC, K là giao điểm thứ hai của AH với đường tròn (O). Đường thẳng đi qua H và vuông góc với OA cắt BC ở I. Chứng minh rằng IK là tiếp tuyến của đường tròn (O)
~~~~~~~~~ Bài làm ~~~~~~~~~
Ta có: \(\widehat{HBD}=\widehat{DAC}\) (Cùng phụ với \(\widehat{ACB}\))
\(\widehat{KBD}=\widehat{DAC}\)( Góc nối tiếp cùng chắn cung \(KC\))
\(\Rightarrow\widehat{HBD}=\widehat{KBD}\)
Ta lại có: \(BD\perp HK\)
\(\Rightarrow BD\) là đường trung trực của \(HK\)
\(\Rightarrow\Delta IHK\) cân tại \(I\)
\(\Rightarrow\widehat{BKD}=\widehat{BHD}=\widehat{AHQ}\)
Lại có:\(\widehat{DKO}=\widehat{HAO}\)( \(\Delta OKA\) cân tại \(O\))
Vì vậy: \(\widehat{DKO}+\widehat{BKD}=\widehat{HAO}+\widehat{AHQ}=90^0\)
\(\Rightarrow\widehat{KIO}=90^0\)
\(\Rightarrow IK\)là tiếp tuyến của đường tròn \(\left(O\right)\)
(Hình vẽ chỉ mang tính chất minh họa cái hình vẽ gần cả tiếng đồng hồ :)) )
Ủa bạn ơi sao phụ nhau? Dòng đầu ấy
Đúng rồi bạn. Phụ nhau ý nghĩa là ^HBD + ^ACB = 90^0 và tương tự như góc kia. (Tam giác vuông ý)
Xem thêm câu trả lời
Cho đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F. Đường tròn tâm O bàng tiếp góc BAC của tam giascABC tiếp xúc với BC và phần kéo dài của các cạnh AB,AC tại P,M,N1. Chứng minh rằng BPCD2. Trên đường thẳng MN lấy các điểm I và K sao cho CK // AB, BI//AC .Chứng minh rằng các tứ giác BICE và BKCF là các hình bình hành.3. Gọi (S) là đường tròn đi qua ba điểm I,K,P. Chứng minh (S) tiếp xúc với các đường thẳng BC,BI,CK
Đọc tiếp
Cho đường tròn tâm O nội tiếp tam giác ABC tiếp xúc với các cạnh BC,CA,AB tương ứng tại D,E,F. Đường tròn tâm O' bàng tiếp góc BAC của tam giascABC tiếp xúc với BC và phần kéo dài của các cạnh AB,AC tại P,M,N
1. Chứng minh rằng BP=CD
2. Trên đường thẳng MN lấy các điểm I và K sao cho CK // AB, BI//AC .Chứng minh rằng các tứ giác BICE và BKCF là các hình bình hành.
3. Gọi (S) là đường tròn đi qua ba điểm I,K,P. Chứng minh (S) tiếp xúc với các đường thẳng BC,BI,CK














