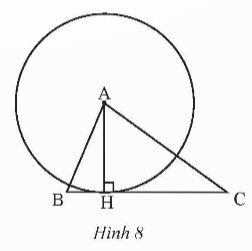
Cho tam giác ABC có đường cao AH (Hình 8). Tìm tiếp tuyến của đường tròn (A; AH) tại H.
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH (H thuộc BC) Vẽ (A;AH) vẽ đường kính HD.Qua D vẽ tiếp tuyến với đường tròn,tiếp tuyến này cắt BA kéo dài tại điểm E
a)CMR: tam giác ADE=tam giác AHB
b)tam giác CBE cân
c) Gọi I là hình chiếu của A trên CE.CMR:CE là tiếp tuyến của đường tròn (A;AH)
hình bạn tự kẻ nha
a> Xét tam giác ADE và tam giác AHB có : góc DAE = HAB(đối đỉnh); góc ADE = góc AHB = 90 độ; AD = AH = bán kính==> tg ADE = AHB (c.g.v_g.n.k)
b> vì tg ADE = AHB ==> AE = AB ==> A là trung điểm của BE (1)
xét tg CBE ta thấy CA vuông góc với AB ==> CA là đường cao (2)
từ (1) và (2) ==> tg CBE cân tại C
c> vì tg CBE cân tại C ==> CA vừa là đường cao vừa là tia pg xuất phát từ đỉnh C ==> góc ACH = ACI
xét tg ACH và tg ACI có: góc AHC = AIC = 90 độ; AC là cạnh chung; góc ACH = ACI(cmt) ==> tg ACH = ACI (c.h_g.n)
=> AH=AI=bán kính (3)
mặt khác AI vuông góc với CE (4)
từ (3) và (4) ==> CE là tiếp tuyến ( khoảng cách từ tâm đến đường thẳng bằng bán kính)
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 15 cm và AC= 8 cm và BC = 17 cm a) Chứng minh tam giác ABC vuôngb) Gọi AH là đường cao trong tam giác ABC, đường thẳng qua H vuông góc với AB cắt đường tròn (A;AH) tại D. Chứng minh BD là tiếp tuyến của đường tròn (A;AH)c) Tính HD.
Bài 1: Cho tam giác ABC vuông tại A, có AB6cm, AC8cm, đường cao AH. Vẽ đường tròn (A,AH). Gọi D,E lần lượt là hình chiếu của H lên AB, ACa/ Tính số đo các góc và độ dài đường cao AH trong tam giác ABCb/ Cm: BC là tiếp tuyến của đường tròn (A) và tứ giác ADHE là hình chữ nhậtc/ Cho HD, HE lần lượt cắt đ. tròn (A) tại P,Q. Cmr: A,P, Q thẳng hàngd/ Cm:AH mũ 2BP.CQe/ Cm: PQ là tiếp tuyến của đường tròn đường kính BC
Đọc tiếp
Bài 1: Cho tam giác ABC vuông tại A, có AB=6cm, AC=8cm, đường cao AH. Vẽ đường tròn (A,AH). Gọi D,E lần lượt là hình chiếu của H lên AB, AC
a/ Tính số đo các góc và độ dài đường cao AH trong tam giác ABC
b/ Cm: BC là tiếp tuyến của đường tròn (A) và tứ giác ADHE là hình chữ nhật
c/ Cho HD, HE lần lượt cắt đ. tròn (A) tại P,Q. Cmr: A,P, Q thẳng hàng
d/ Cm:AH mũ 2=BP.CQ
e/ Cm: PQ là tiếp tuyến của đường tròn đường kính BC
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
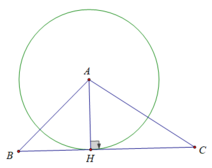
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
Đúng 0
Bình luận (0)
Cho tam giác ABC, đường cao AH. Chứng minh rằng đường thẳng BC là tiếp tuyến của đường tròn (A; AH).
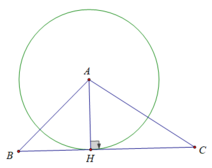
Ta có: BC đi qua điểm H thuộc đường tròn (A; AH)
BC ⊥ AH tại H
⇒ BC là tiếp tuyến của đường tròn (A; AH)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A và có đường cao AH = 3cm. Vẽ đường tròn (A ; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn tại D cắt AC ở E.
Mọi người vẽ hình giùm emvới em cảm ơn nhiều
Cho tam giác abc có đường cao AH. Vẽ đường tròn tâm A, bán kính AH kẻ tiếp tuyến CD với đường tròn a) chứng minh BC là tiếp tuyến của ( A,AH) b) chứng minh AC lớn hơn hoặc bằng DH c) vẽ đường kính HK của (A,AH). Chứng minh DK//AC
Cho tam giác ABC vuông tại A đường cao AH biết AB = 6 cm AC bằng 8 cm Tính ah BH chứng minh CB là tiếp tuyến của đường tròn A phẩy
a: BC=10cm
AH=6*8/10=4,8cm
BH=AB^2/BC=3,6cm
b: Vì BH vuông góc với AH tại H
nên CB là tiếp tuyến của (A'AH)
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông ở A,đường cao AH. Vẽ đường tròn tâm A, bán kính AH. Gọi HD là đường kính đường tròn (A:AH). Tiếp tuyến của đường tròn tại D cắt CA ở E. Gọi I là hình chiếu của A trên BE. Chứng minh rằng:
a)Tam giác giác BEC cân
b)AI=AH
c)BE là tiếp tuyến của đường tròn (A:AH)
d)BE=BH + DE
Cho tam giác ABC vuông tại A; đường cao AH. Vẽ đường tròn (A; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn D cắt CA ở E.a. CMR BE tiếp xúc với đường tròn (A) tại một điểm gọi là I và IA là tiếp tuyến của đường tròn đường kính BC.b. EA cắt đường tròn (A) tại T và S(ETES) và cắt DI tại N. CM T là tâm đường tròn nội tiếp của tam giác EDI và TN.SETE.SN.c/ Đường thẳng vuông góc với ED tại E cắt đường thẳng AI tại M. CM AE22AI.AMmn giúp e với ạ, e đang cần gấp
Đọc tiếp
Cho tam giác ABC vuông tại A; đường cao AH. Vẽ đường tròn (A; AH). Gọi HD là đường kính của đường tròn đó. Tiếp tuyến của đường tròn D cắt CA ở E.
a. CMR BE tiếp xúc với đường tròn (A) tại một điểm gọi là I và IA là tiếp tuyến của đường tròn đường kính BC.
b. EA cắt đường tròn (A) tại T và S(ET<ES) và cắt DI tại N. CM T là tâm đường tròn nội tiếp của tam giác EDI và TN.SE=TE.SN.
c/ Đường thẳng vuông góc với ED tại E cắt đường thẳng AI tại M. CM AE2=2AI.AM
mn giúp e với ạ, e đang cần gấp