Cho A= 1: (x+2 / x căn x -1 - căn x+1/x-1 + căn x+1/x+ căn x+1
a) rút gọn A
b) với x>0 và x+1 : chứng minh A >3

Những câu hỏi liên quan
Rút gọn biểu thức
A= căn x+1 B=4 căn x/x+4 A=x-căn x+1
A=3 /2 căn x A=3/căn x+3
A=1-căn x A=x-2 căn x-1
\(A=\sqrt{x}+1\) (đã thu gọn)
\(B=\dfrac{4\sqrt{x}}{x+4}\) (đã thu gọn)
\(A=x-\sqrt{x}+1=\sqrt{x}\cdot\sqrt{x}-\sqrt{x}+1=\sqrt{x}\left(\sqrt{x}-1\right)+1\)
\(A=\dfrac{3}{2\sqrt{x}}\) (đã thu gọn)
\(A=\dfrac{3}{\sqrt{x}+3}\) (đã thu gọn)
\(A=1-\sqrt{x}\) (đã thu gọn)
\(A=x-2\sqrt{x}-1=\sqrt{x}\left(\sqrt{x}-2\right)-1\)
Đúng 1
Bình luận (0)
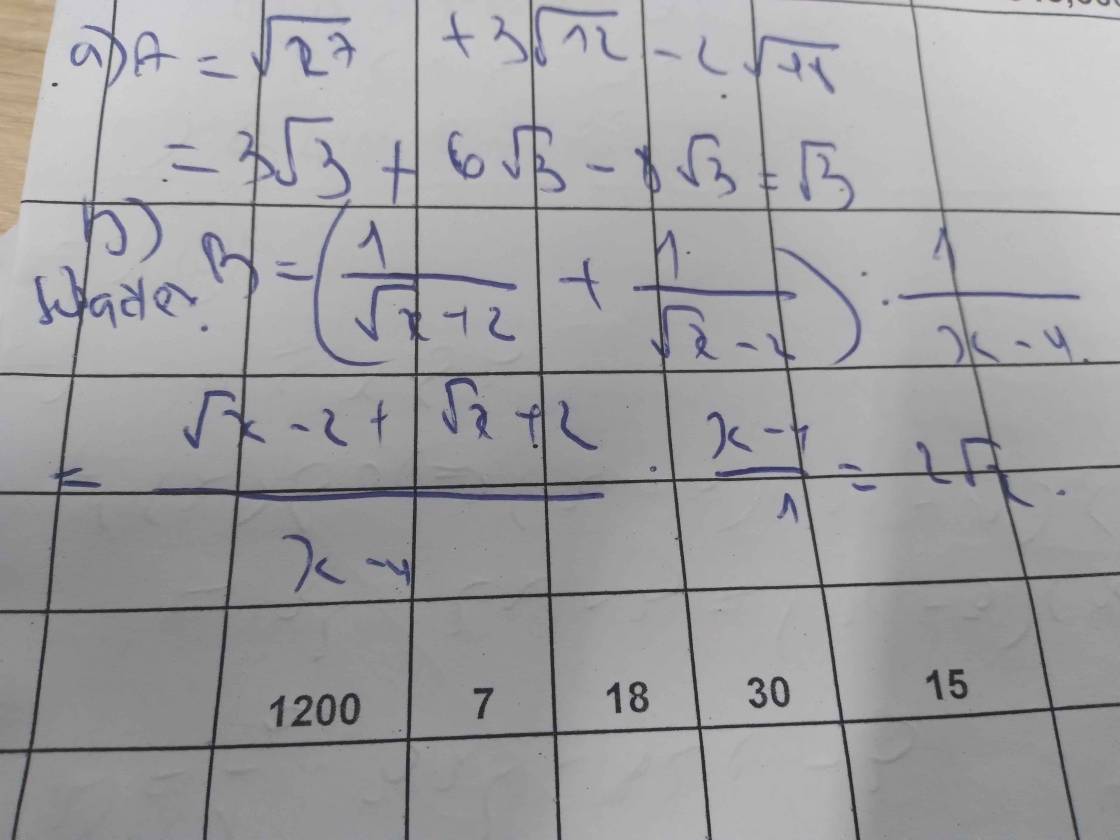
Rút Gọn Bt sau : a, A=căn27 + 3 căn 12 -2 căn 48 b, B= ( 1trên Căn x +2 + 1 trên Căn x-2 ) Chia 1 trên căn x-4 ; Với X lớn hơn 0; x #4
Cho P =(căn x)/(căn x-1)-(2 căn x)/(căn x+1)+(x-3)/(x-1) a) tìm ĐKXĐ b) rút gọn P
`a)->` ĐKXĐ : `x>=0;x\ne1`
`b)` Ta có :
`P=(\sqrtx)/(\sqrtx-1)-(2\sqrtx)/(\sqrtx+1)+(x-3)/(x-1)`
`P=(\sqrtx(\sqrtx+1)-2\sqrtx(\sqrtx-1)+x-3)/(x-1)`
`P=(x+\sqrtx-2x+2\sqrtx+x-3)/(x-1)`
`P=(3\sqrtx-3)/(x-1)`
`P=(3(\sqrtx-1))/((\sqrtx-1)(\sqrtx+1))`
`P=3/(\sqrtx+1)`
Vậy `P=3/(\sqrtx+1)` khi `x>=0;x\ne1`
Đúng 2
Bình luận (3)
\(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}+1}+\dfrac{x-3}{x-1}\\ =\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{2\sqrt{x}}{\sqrt{x}+1}+\dfrac{x-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}-\dfrac{2\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{x-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{x+\sqrt{x}-2x+2\sqrt{x}+x-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{3\sqrt{x}-3}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{3\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\\)
\(=\dfrac{3}{\sqrt{x}+1}\)
Bổ sung \(\text{đ}k\text{x}\text{đ}:x\ge0;x\ne1\)
Đúng 1
Bình luận (3)
b1 : rút gọn biểu thức
a: x-y/y^2 nhân căn y^4/x^2 - 2xy + y^2 với x khác y
b: căn x- 2 căn x +1/x+ 2 căn x +1 với x > 0
b2: rút gọn rồi tính giá trị
a: B= căn (x+2) ^4 / (3-x)^2 + x^2+1/x+3 với x<3 và tính b khi x= 0.5
b: C = 5x - căn 8 + căn x^3 + 2x^2/ căn x+2 cới x > -2 và tính C khi x + - căn 2
c: D= căn 3(x+y)^2/4 nhân 2/x^2-y^2 với x khác y
cho A= (1/1- căn x + 1/1 + căn x) : (1/1- căn x -1/ 1+ căn x) + 1/1- căn x
a) tìm dkxd và rút gọn A
b. tính giá trị của A khi x= 7+ 4 căn 3
c. với giá trị nào của x thì A đạt giá trị nhỏ nhất
a, \(A=\left(\frac{1}{1-\sqrt{x}}+\frac{1}{1+\sqrt{x}}\right):\left(\frac{1}{1-\sqrt{x}}-\frac{1}{1+\sqrt{x}}\right)+\frac{1}{1-\sqrt{x}}\)ĐK : \(x>0;x\ne1\)
\(=\left(\frac{1+\sqrt{x}+1-\sqrt{x}}{1-x}\right):\left(\frac{1+\sqrt{x}-1+\sqrt{x}}{1-x}\right)+\frac{1}{1-\sqrt{x}}\)
\(=\frac{2}{1-x}.\frac{1-x}{2\sqrt{x}}+\frac{1}{1-\sqrt{x}}=\frac{1}{\sqrt{x}}+\frac{1}{1-\sqrt{x}}=\frac{1-\sqrt{x}+\sqrt{x}}{-x+\sqrt{x}}=\frac{1}{\sqrt{x}-x}\)
b, Ta có : \(x=7+4\sqrt{3}=7+2.2\sqrt{3}=\left(\sqrt{4}+\sqrt{3}\right)^2\)
\(A=\frac{1}{\sqrt{4}+\sqrt{3}-7+4\sqrt{3}}\)
bài 1rút gọn bt a, 2 căn 10 - 5 trên 4 - căn 10 b, (2/3 căn 3) - (1/4 căn 18) + (2/5 căn 2) - 1/4 căn 12 bài 2:c/m các đẳng thức : [căn x + căn y trên căn x - căn y) - ( căn x - căn y trên căn x + căn y) : căn xy trên x-y =4 bài 3: cho B={[2 căn x trên căn x +3] + [ căn x trên căn x - 3] - 3[ căn x +3] trên x-9} : { [ 2 căn x -2 trên căn x -3] -1} a, rút gọn b, tìm x để P<-1 Mọi ng giúp mk nhé
cho A= ( 1/căn x+1 - 2 căn x-2/ x căn x- căn x+x -1):( 1/căn x-1- 2/ x-1)
a) rút gọn A
b)tìm x thuộc Z để A thuộc Z
c)tìm x để A đạt GTNN
giúp mình vs ạ
a: \(A=\left(\dfrac{1}{\sqrt{x}+1}-\dfrac{2\sqrt{x}-2}{x\sqrt{x}+x-\sqrt{x}-1}\right):\left(\dfrac{1}{\sqrt{x}-1}-\dfrac{2}{x-1}\right)\)
\(=\dfrac{x-1-2\sqrt{x}+2}{\left(\sqrt{x}+1\right)\left(x-1\right)}:\dfrac{\sqrt{x}+1-2}{x-1}\)
\(=\dfrac{x-2\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(x-1\right)}\cdot\dfrac{x-1}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}\)
b: Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}+1\)
=>\(\sqrt{x}+1-2⋮\sqrt{x}+1\)
=>căn x+1 thuộc {1;2}
=>căn x thuộc {0;1}
mà x<>1
nên x=0
Đúng 0
Bình luận (0)
A=x căn x-1/x - căn x - x căn x+1/x + căn x+(căn x-1/ căn x). (căn x+1/ căn x-1+ căn x-1/ căn x+1)
rút gọn A
rút gọn A=((1/x- căn x) +(1/căn x -1)) / ((căn x+1)/(căn x -1)^2)
tìm GTLN của P=A-16 căn x
`A=(1/(x-sqrtx)+1/(sqrtx-1)):(sqrtx+1)/(sqrtx-1)^2`
`=((sqrtx+1)/(x-sqrtx)).(sqrtx-1)^2/(sqrtx+1)`
`=(sqrtx-1)^2/(x-sqrtx)`
`=(sqrtx-1)/sqrtx`
Đúng 0
Bình luận (0)