(Dựa vào hình vẽ có được sau HĐ3). Bằng cách xét hai tam giác OMA và OMB, chứng minh rằng:
a) MA = MB;
b) MO là tia phân giác của góc AMB;
c) OM là tia phân giác của góc AOB.
chox xOy bằng 120 độ Trên tia Ox lấy điểm M (M khác O) Vẽ tia Ma nằm trong góc xOy sao cho OMa bằng 60 độ a) Chứng minh MA song song với Oy b)Vẽ tia MB là tia đối của tia Ma. Tính OMb c) kẻ Ot là tia phân giác của góc xOy ,Mz là tia phân giác của góc OMb. chứng minh Ot song song với mz
Cho góc xOy nhọn, Ot là tia phân giác của góc xOy lấy M thuộc Ot. Kẻ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B a) chứng minh: tam giác OMA=tam giác OMB b)Gọi I là giao điểm của AB và OM:Chứng minh tam giác AMB cân c) Chứng minh: OM mũ 2 =OI mũ 2 + IM mũ 2 + 2AI mũ 2
A)Vì OT là phân giác của góc xoy => O1=O2
-Xét tam giác OAM và tam giác OBM:
O1=O2
OM chung
=> tam giác OAM = tam giác OBM(c.huyền và góc nhọn)
B) vì MA=MB (đ.án câu a)
=>AMB là tam giác cân tại M
C) ko biết :))
Cho xOy 1200 . Trên tia Ox lấy điểm M ( M O). Vẽ tia Ma nằm trong
góc xOy sao cho OMa 600 .
a) Chứng minh Ma // Oy.
b) Vẽ tia Mb là tia đối của tia Ma. Tính OMb ?
c) Kẻ Ot là tia phân giác của góc xOy; Mz là tia phân giác của góc OMb.
Chứng minh Ot//Mz.
GIÚP MÌNH NHA
ありがとう
gọi OT la tia phân giác của góc xOy . Trên tia Ot lấy điem M kẻ MA vuông góc Ox MB vuông góc Oy
a) chứng minh tam giác OmA=OMB và tam giác OBA cân
b) gọi I là giao điểm của AB và OM chứng minh IA =IB va OM vuông góc AB
Vì Ot là tia phân giác của ^xOy, mà M thuộc Ot=>Om là tia phân giác của ^AOB
a) xét tam giác OAM và tam giác OBM có:
OM:cạnh chung
^AOM=^BOM( vì OM là tia phân giác của ^AOB)
=>tam giác....=tam giác...(ch-gn)
=>OA=OB(cặp cạnh t.ứ)
=>tam giác OBA cân tại O ( dấu hiệu nhận biết)
b)xét tam giác OAI=tam giác OBI(ch-gn)=>IA=IB
Vì OM là tia phân giác của ^AOB, mà I thuộc OM
=>OI là tia phân giác của ^AOB
Xét tam giác OBA cân tại O có:OI là tia phân giác của ^AOB
=>OI cũng là đg trung trực của AB
=>OM là đg trung trưc của AB
=>OM _|_ AB
Giúp em với ạ!!
Cho góc nhọn xOy có tia phân giác Ot. Trên tia Ot lấy điểm M. Vẽ MA vuông góc với Ox tại A, MB vuông góc với Oy tại B
a. Gọi L là giao điểm của AB với Ot. Tính OM
b. Vẽ HE song song với OB (E thuộc OA). Chứng minh tam giác AHE cân.
P/s: Biết tam giác OMA = tam giác OMB
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2 = ab) như trong hai hình sau:
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nữa cạnh đó thì tam giác ấy là tam giác vuông.
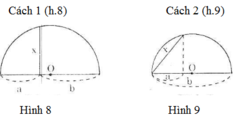
- Cách 1: (h.8)
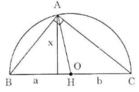
Theo cách dựng, ΔABC có đường trung tuyến AO bằng một nửa cạnh BC, do đó ΔABC vuông tại D.
Vì vậy AH2 = BH.CH hay x2 = ab
Đây chính là hệ thức (2) hay cách vẽ trên là đúng.
- Cách 2: (h.9)
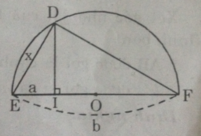
Theo cách dựng, ΔDEF có đường trung tuyến DO bằng một nửa cạnh EF, do đó ΔDEF vuông tại D.
Vậy DE2 = EI.EF hay x2 = a.b
Đây chính là hệ thức (1) hay cách vẽ trên là đúng.
Người ta đưa ra hai cách vẽ đoạn trung bình nhân x của hai đoạn thẳng a, b (tức là x2 = ab) như trong hai hình sau:
Dựa vào các hệ thức (1) và (2), hãy chứng minh các cách vẽ trên là đúng.
Gợi ý: Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nữa cạnh đó thì tam giác ấy là tam giác vuông.
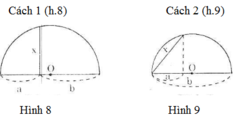
- Cách 1: (h.8)
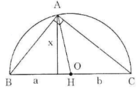
Theo cách dựng, ΔABC có đường trung tuyến AO bằng một nửa cạnh BC, do đó ΔABC vuông tại D.
Vì vậy AH2 = BH.CH hay x2 = ab
Đây chính là hệ thức (2) hay cách vẽ trên là đúng.
- Cách 2: (h.9)
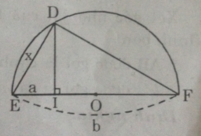
Theo cách dựng, ΔDEF có đường trung tuyến DO bằng một nửa cạnh EF, do đó ΔDEF vuông tại D.
Vậy DE2 = EI.EF hay x2 = a.b
Đây chính là hệ thức (1) hay cách vẽ trên là đúng.
Cho góc nhọn xOy có Ot là tia phân giác. Trên tia Ot lấy điểm M,kẻ MA vuông góc Chứng minh: tam giác OMA=tam giác OMB Chứng minh Om là đường trung trực của đoạn ab Gọi H,k lần lượt là giao điểm của AM với tia Oy và BM với tia Ox chứng minh ab // hk
Xét ΔOMA vuông tại M và ΔOMB vuông tại M có
OA=OB
OM chung
Do đó: ΔOMA=ΔOMB
Cho góc nhọn xOy . Trên tia phân giác Ot của góc xOy lấy điểm M . Từ M hạ các đường vuông góc MA \(\perp\)Ox và MB \(\perp\)Oy ( A \(\in\)Ox ; B \(\in\)Oy )
a) Chứng minh rằng tam giác OMA = tam giác OMB
b) Chứng minh rằng 2 tam giác OAB và MAB là 2 tam giác cân
Cho góc nhọn xOy . Trên tia phân giác Ot của góc xOy lấy điểm M . Từ M hạ các đường vuông góc MA \(⊥\)Ox và MB \(⊥\)Oy ( A \(∈\)Ox ; B \(∈\)Oy )
a) Chứng minh rằng tam giác OMA = tam giác OMB
b) Chứng minh rằng 2 tam giác OAB và MAB là 2 tam giác cân
a, Vì Ot là phân giác của xOy
=> xOt = tOy = xOy/2
Xét △OAM vuông tại A và △OBM vuông tại B
Có: AOM = MOB
OM là cạnh chung
=> △OAM = △OBM (cgv-gn)
b, Vì △OAM = △OBM
=> OA = OB (2 cạnh tương ứng)
=> AM = BM (2 cạnh tương ứng)
Xét △OAB có: OA = OB
=> △OAB cân tại O
Xét △ABM có: AM = BM
=> △ABM cân tại M