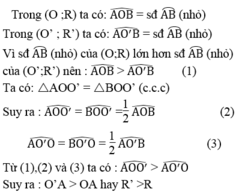Tại sao số đo cung lớn của một đường tròn luôn lớn hơn 180°?

Những câu hỏi liên quan
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
a) Đúng. Dựa vào cách so sánh hai cung (SGK trang 68).
Chú ý: Khi ta nói hai cung bằng nhau, nghĩa là hai cung này so sánh được (tức chúng cùng nằm trong một đường tròn hoặc trong hai đường tròn bằng nhau). Do đó, theo cách so sánh hai cung đã biết thì hai cung bằng nhau thì số đo bằng nhau.
b) Sai. Nếu hai cung này nằm trong hai đường tròn có bán kính khác nhau thì ta không thể so sánh hai cung.
c) Sai. (Lí luận như câu b)
d) Đúng. (Lí luận như câu a)
Đúng 0
Bình luận (0)
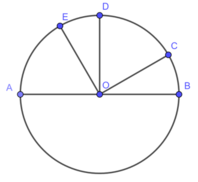
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ
∠
BC
1
6
sđ
∠
BA; sđ
∠
BD
1
2
sđ
∠
BA; sđ
∠
BE
2
3
sđ
∠
BA. Đọc tên các góc ở tâm có số đo không lớn hơn...
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho sđ ∠ BC = 1 6 sđ ∠ BA; sđ ∠ BD = 1 2 sđ ∠ BA; sđ ∠ BE = 2 3 sđ ∠ BA. Đọc tên các góc ở tâm có số đo không lớn hơn 180 °
Mỗi khẳng định sau đây đúng hay sai? Vì sao?
a) Hai cung bằng nhau thì có số đo bằng nhau.
b) Hai cung có số đo bằng nhau thì bằng nhau.
c) Trong hai cung, cung nào có số đo lớn hơn là cung lớn hơn.
d) Trong hai cung trên một đường tròn, cung nào có số đo nhỏ hơn thì nhỏ hơn.
a) Đúng
b) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
c) Sai. Không rõ hai cung nằm trên một đường tròn hay trên hai đường tròn bằng nhau không.
Đúng 0
Bình luận (1)
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho số đo cung BCdfrac{1}{6} số đo cung BA, số đo cung BDdfrac{1}{2} số đo cung BA, số đo cung BEdfrac{2}{3} số đo cung BA.
a) Đọc tên các góc ở tâm số đo không lớn hơn 180^0
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn 180^0)
d) So sánh hai cung nhỏ AE và BC
Đọc tiếp
Cho đường tròn tâm O đường kính AB. Các điểm C, D, E cùng thuộc một cung AB sao cho số đo cung \(BC=\dfrac{1}{6}\) số đo cung BA, số đo cung \(BD=\dfrac{1}{2}\) số đo cung BA, số đo cung \(BE=\dfrac{2}{3}\) số đo cung BA.
a) Đọc tên các góc ở tâm số đo không lớn hơn \(180^0\)
b) Cho biết số đo của mỗi góc ở tâm tìm được ở câu trên
c) Cho biết tên của các cặp cung có số đo bằng nhau (nhỏ hơn \(180^0\))
d) So sánh hai cung nhỏ AE và BC
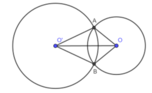
Cho hai đường tròn (O; R) và (O': R) cắt nhau tại A, B. Hãy so sánh R và R' trong các trường hợp sau :
a) Số đo cung nhỏ AB của (O;R) lớn hơn số đo cung nhỏ AB của (O'; R')
b) Số đo cung lớn AB của (O;R) nhỏ hơn số đo cung lớn AB của (O'; R')
c) Số đo hai cung nhỏ bằng nhau.
Cho hai đường tròn đồng tâm (O;R) và (O; ). Trên đường tròn nhỏ lấy một điểm M . Tiếp tuyến tại M của đường tròn nhỏ cắt đường tròn lớn tại A và B. Tia OM cắt đường tròn lớn tại C. a) Chứng minh rằng = ( cung CA bằng cung CB) b) Tính số đo của hai cung AB
Cho hai đường tròn (O; R) và (O’ ; R’) cắt nhau tại A ,B .Hãy so sánh R và R’ trong các trường hợp sau: Số đo cung nhỏ AB của (O ;R) lớn hơn số đo cung nhỏ AB của (O’ ;R’)
Từ một điểm a trên đường tròn tâm o vẽ tiếp tuyến ax trên đường tròn lấy điểm b ,OB cắt tia ax tại điểm m sao cho góc amo = 36 độ tính số đo cung AB nhỏ và cung AB lớn
góc AOB=90-36=54 độ
=>sđ cung AB nhỏ=54 độ
sđ cung AB lớn=360-54=306 độ
Đúng 0
Bình luận (0)
Hai tiếp tuyến của đường tròn O tại A và B cách nhau tại P. Biết góc APB = 55 độ
a) số đo mỗi cung AB
b) gọi M là bán kính của đường tròn tâm O sao cho OM song song với PB, Mthuộc cung lớn AB. Tính số đo cung AM
a) tứ giác APBQ có góc OAP=90độ, OBP=90 độ ( zì PA , PB tiếp tuyến )
góc APB =55 độ
góc AOB =360 độ -90-90-55=125
=> cung nhỏ AB là 125 độ
cung lớn AB là
360-125=235 độ
Cho đường tròn tâm O và dây cung BC. Điểm A di chuyển trên cung lớn BC sao cho tam giác ABC có 3 góc nhọn. Đường cao BE, CF của tam giác ABC cắt nhau tại H và cắt đường tròn theo thứ tự tại M và N. Cho cung BC nhỏ có số đo bằng 120 độ. Tính tỉ số diện tích của tam giác AEF và tứ giác BCEF