Cho đường tròn đường kính BC. Chứng minh rằng với điểm A bất kì (khác B và C) trên đường tròn, ta đều có: BC < AB + AC < 2BC.

Những câu hỏi liên quan
Cho đường tròn (O) đường kính BC, từ điểm A bất kì nằm trên đường tròn ( A khác B,C ) vẽ tiếp tuyến với đường tròn, tiếp tuyến này cắt 2 tiếp tuyết tại B và C của đường tròn lần lượt tại M và N. Chứng minh OM // AC
ta có na=nc => n thuộc trung trực của ac
ta có: oa=oc => o thuộc trung trực của ac
suy ra: on là trung trực của ac => on vuông góc với ac
ta có mo vuông góc với on ( tính chất tia phân giác của 2 góc kề bù )
Suy ra: om//ac (cùng vuông góc với on)
Đúng 0
Bình luận (0)
1/Cho nửa đường tròn (o) đường kính AB. C là 1 điểm bất kì trên nữa đường tròn sao cho C khác A và AC<CB điểm D thuộc cung nhỏ BC sao cho COD=90 độ. gọi E là gđ của AD và BC, F là gđ của AC vào BD
a) Chứng minh CEDF là tứ giác nội tiếp
b) Chứng minh FCEA là tứ giác nội tiếp
c) Gọi I là trung điểm của EF. chứng minh IC là tiếp tuyến của (o)
a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
1/Cho nửa đường tròn (o) đường kính AB. C là 1 điểm bất kì trên nữa đường tròn sao cho C khác A và AC<CB điểm D thuộc cung nhỏ BC sao cho COD=90 độ. gọi E là gđ của AD và BC, F là gđ của AC vào BD
a) Chứng minh CEDF là tứ giác nội tiếp
b) Chứng minh FCEA là tứ giác nội tiếp
c) Gọi I là trung điểm của EF. chứng minh IC là tiếp tuyến của (o)
a: góc ACB=1/2*180=90 độ
=>góc FCE=90 độ
góc ADB=1/2*180=90 độ
=>gó FDE=90 độ
Vì góc FCE+góc FDE=180 độ
nên FCED nội tiếp
b: Đề sai rồi bạn vì F,C,A thẳng hàng
c: góc ICO=góc ICE+góc OCE
=góc IEC+góc OBE
=90 độ-góc CBA+góc CBA
=90 độ
=>CI là tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Cho nửa đường tròn (O;R) đường kính AB và 1 điểm C trên nửa đường tròn đó (AC<BC),H là 1 điểm bất kì trên dây BC nhưng không trùng với B và C; AH cắt nửa đường tròn tại điểm thứ 2 là D, AC cắt đường thẳng BD tại E
a, Chứng minh tứ giác CHDE nội tiếp
b, Vẽ tiếp tuyến Bx của đường tròn (O); tia CD cắt Bx tại M. Chứng minh: MB^2=MC.MD
c, Chứng minh góc CHE= góc BAC
a: góc ACB=góc ADB=1/2*180=90 độ
=>BC vuông góc AE,AD vuông góc BE
góc ECH+góc EDH=180 độ
=>ECHD nội tiếp
b: Xét ΔMBD và ΔMCB có
góc MBD=góc MCB
góc BMD chung
=>ΔMBD đồng dạng với ΔMCB
=>MB/MC=MD/MB
=>MB^2=MC*MD
Đúng 0
Bình luận (0)
Giúp mik với :((( Cho đường tròn tâm O bán kính R và hai đường kính AB, CD vuông góc với nhau. Điểm M bất kì thuộc cung nhỏ BC (với M khác B và C). Gọi I là giao điểm của AM và BC, J là hình chiếu của I trên AB. Chứng minh rằng: a) Tứ giác BMIJ là tứ giác nội tiếp b) JI là phân giác của góc CJM c) J, M, D thẳng hàng
Nếu đc thì các bạn vẽ hình giúp mik với ;-;
Mik cảm ơn ;-;
a: Xét (O) có
ΔAMB nội tiếp
AB là đường kính
=>ΔAMB vuông tại M
Xét tứ giác BMIJ có
góc IJB+góc IMB=180 độ
=>BMIJ là tứ giác nội tiếp
b: BMIJ là tứgiác nội tiếp
=>góc MJI=góc MBI
Xét tứ giác CAJI có
góc ACI+góc AJI=180 độ
=>CAJI là tứ giác nội tiêp
=>góc CJI=góc CAI
góc MJI=góc MBI
mà góc CAI=góc MBI
nên góc CJI=góc MJI
=>JI là phân giác của góc CJM
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A. Nửa đường tròn đường kính AB cắt cạnh BC tại điểm D (khác B). Lấy điểm E bất kì trên cung nhỏ AD (E không trùng với A và D). BE cắt cạnh AC tại điểm F. Chứng minh rằng CDEF là tứ giác nội tiếp.
Dễ thấy \(\Delta AFE~\Delta BAE\left(g.g\right)\)
\(\Rightarrow\widehat{AFE}=\widehat{BAE}\)
mà \(AEDB\)nội tiếp nên \(\widehat{BAE}+\widehat{BDE}=180^o\)
\(\Rightarrow\widehat{AFE}+\widehat{BDE}=180^o\)
\(\Rightarrow\widehat{CFE}+\widehat{CDE}=180^o\)
suy ra \(CDEF\)nội tiếp.
4.Cho đường tròn (O) đường kính BC. Lấy điểm A bất kì nằm trên đường tròn( AB AC ) . Gọi M là giao điểm của tiếp tuyến tại A với đường thẳng BC. Chứngminh rằng: gócBAO góc CAM5. Cho hai đường tròn (O) và (O) cắt nhau tại A và B. Tiếp tuyến kẻ từ A của ( O)cắt (O) tại C và tiếp tuyến tại A của (O) cắt (O) tại D. Chứng minh rằng:góc CBA góc DBA
Đọc tiếp
4.Cho đường tròn (O) đường kính BC. Lấy điểm A bất kì nằm trên đường tròn
( AB> AC ) . Gọi M là giao điểm của tiếp tuyến tại A với đường thẳng BC. Chứng
minh rằng: gócBAO = góc CAM
5. Cho hai đường tròn (O) và (O') cắt nhau tại A và B. Tiếp tuyến kẻ từ A của ( O')
cắt (O) tại C và tiếp tuyến tại A của (O) cắt (O') tại D. Chứng minh rằng:
góc CBA = góc DBA
cho nửa đường tròn tâm o đường kính ab trên nửa đường tròn lấy điểm c sao cho ca <cb,vẽ ch vuông góc với ab (h thuộc ab).trên cung bc lấy điểm d bất kì (d khác b và c),gọi e là giao diểm của ch và ad.
a)chứng minh tứ giác bdhe nội tiếp đường tròn
b)chứng minh ac bình phương = ae.ad
a: góc EHB+góc EDB=180 độ
=>BDHE nội tiếp
b: Xét ΔACE và ΔADC có
góc ACE=góc ADC
góc CAE chung
=>ΔACE đồng dạng với ΔADC
=>AC^2=AE*AD
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O có đường kính AB. Gọi M là điểm bất kì thuộc nửa đường tròn, H là chân đường vuông góc kẻ từ M đén AB. Vẽ đường tròn (M; MH). Kẻ các tiếp tuyến AC, BD với đường tròn tâm M (C và D là các tiếp điểm khác H). Chứng minh rằng khi điểm M di chuyển trên nửa đường tròn (O) thì tổng AC + BD không đổi
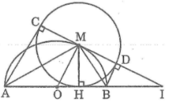
Trong đường tròn (M; MH), theo tính chất hai tiếp tuyến cắt nhau, ta có:
AC = AH và BD = BH
Khi M thay đổi trên nửa đường tròn tâm O thì AC luôn bằng AH và BD luôn bằng BH
Suy ra: AC + BD = AH + BH = AB không đổi
Đúng 0
Bình luận (0)
Cho nửa đường tròn tâm O, đường kính AB = 2R. Trên nửa đường tròn lấy điểm C bất kì (C khác A và B). Tiếp tuyến tại C và tiếp tuyến tại A cắt nhau tại M. a) Chứng minh bốn điểm, O, A, M, C cùng thuộc một đường tròn. b) AC cắt OM tại H, chứng minh AC vuông góc với OM và 2.OH OM =R mũ 2.
a: Xét tứ giác OAMC có
\(\widehat{OAM}+\widehat{OCM}=180^0\)
Do đó: OAMC là tứ giác nội tiếp
Đúng 0
Bình luận (0)

















