cho tam giác abc là tam giác đều . tính số do mỗi góc của tam giác đó.

Những câu hỏi liên quan
Cho tam giác đều ABC. Tính số đo mỗi góc của tam giác đó.
Số đo mỗi góc của tam giác đều bằng \(\dfrac{{180}}{3} = 60^\circ \).
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn. Vẽ về phía ngoài tam giác đó các tam giác đều ABD và ACE. Gọi H là giao điểm của BE và CD. Tính số đo góc BHC
Cho tam giác ABC có số đo góc là A; B; C lần lượt tỉ lệ với 2;3;4. Tính số đo mỗi góc của tam giác đó.
Gọi 3 góc A; B; C lần lượt là x; y; z (x; y; z >0)
Ta có: x + y + z = 1800 (tổng 3 góc trong của tam giác)
Vì x; y; z lần lượt tỉ lệ với 2; 3; 4 => \(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}\)
Áp dụng tính chất dãy tỉ số bằng nhau, ta có:
\(\frac{x}{2}=\frac{y}{3}=\frac{z}{4}=\frac{x+y+z}{2+3+4}=\frac{180}{9}=20\)
=> \(\frac{x}{2}=20=>x=20.2=40\)
\(\frac{y}{3}=20=>y=20.3=60\)
\(\frac{z}{4}=20=>z=20.4=80\)
Vậy:
Góc A bằng 400
Góc B bằng 600
Góc C bằng 800
Đúng 1
Bình luận (0)
Giải
Gọi số đo góc A;B;C; lần lược là a;b;c ( a;b;c thuộc Z;a,b,c khác 0)
Vì số đo góc A;B;C tỉ lệ với các số 2;3;4 nên ta có: \(\frac{a}{2}\) = \(\frac{b}{3}\) = \(\frac{c}{4}\)
Theo tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{a}{2}\) = \(\frac{b}{3}\) =\(\frac{c}{4}\) = \(\frac{a+b+c}{2+3+4}\)=\(\frac{180}{9}\)=20
\(\frac{a}{2}\) =20=>a=2.20=40
=> { \(\frac{b}{3}\) =20=>b=3.20=60
\(\frac{c}{4}\) =20=>c=4.20=80
Vậy a=40;b=60;c=80
=>Góc A=40 độ, góc B=60 độ,gócC= 80 độ
Đúng 0
Bình luận (0)
cho tam giác ABC, vẽ phía ngoài tam giác đó các tam giác đều ABE và ACF. Gọi K, L lần lượt là trung điểm của EB và CF, M là điểm thuộc cạnh BC sao cho BM=3MC. Tính số đo các góc của tam giác KLM
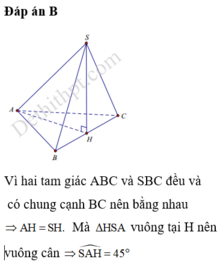
Cho hình chóp SABC có đáy ABC là tam giác đều cạnh a Hình chiếu vuông góc của S lên (ABC )trùng với trung điểm H của cạnh BC biết tam giác SBC là tam giác đều tính số đo của góc giữa SA và (ABC)
\(SH\perp\left(ABC\right)\Rightarrow\widehat{SAH}\) là góc giữa SA và (ABC)
\(SH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều SBC cạnh a)
\(AH=\dfrac{a\sqrt{3}}{2}\) (đường trung tuyến trong tam giác đều ABC cạnh a)
\(tan\widehat{SAH}=\dfrac{SH}{AH}=1\Rightarrow\widehat{SAH}=45^0\)
Đúng 2
Bình luận (0)
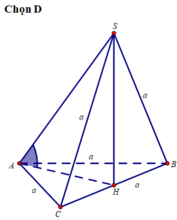
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC) A. 300 B. 450 C. 600 D. 900
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC)
A. 300
B. 450
C. 600
D. 900
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên
(
A
B
C
)
trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và
(
A
B
C
)
.
A.
30
0
B.
45
0
C.
60
0
D. ...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên ( A B C ) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và ( A B C ) .
A. 30 0
B. 45 0
C. 60 0
D. 90 0
Đáp án B
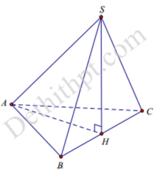
Vì hai tam giác ABC và SBC đều và có chung cạnh BC nên bằng nhau ⇒ A H = S H .
Mà Δ H S A vuông tại H nên vuông cân
⇒ S A H ^ = 45 °
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của S lên (ABC) trùng với trung điểm H của cạnh BC. Biết tam giác SBC là tam giác đều. Tính số đo của góc giữa SA và (ABC).
A. 30 °
B. 75 °
C. 60 °
D. 45 °
Gọi cho là ai trọng tâm của tam giác đều ABC cạnh 2 cm chứng minh cách đều ba cạnh của tam giác ABC từ đó tính khoảng cách từ G tới mỗi canh của 1 tam giác
Bài 1: cho tam giác abc,có góc A60 độ. DỤNG ra ngoài các tam giác đó các tam giác đều ABM,CAN.A) CM 3 điểm: M,N,A thẳng hàgB)Cm: BNCMC) gọi O là giao điểm của BN,CM. Tính góc BOCBài 2 : Cho tam giác abc đều, D thuộc BC( tùy ý), Từ D kẻ các đg thẳng // với AB,AC cắt AB,AC lần lượt tại E,F A) So sánh BF, CEB) Gọi P,Q lần lượt là trung điểm của CE,BF. Tam giác PQD là tam giác j? Chứng minh Bài 8 cho tam giác ABC, phân giác AK. GIAO 3 đường phân giác của tam giác ABK cách đều 3 đỉnh của tam giác AB...
Đọc tiếp
Bài 1: cho tam giác abc,có góc A=60 độ. DỤNG ra ngoài các tam giác đó các tam giác đều ABM,CAN.
A) CM 3 điểm: M,N,A thẳng hàg
B)Cm: BN=CM
C) gọi O là giao điểm của BN,CM. Tính góc BOC
Bài 2 : Cho tam giác abc đều, D thuộc BC( tùy ý), Từ D kẻ các đg thẳng // với AB,AC cắt AB,AC lần lượt tại E,F
A) So sánh BF, CE
B) Gọi P,Q lần lượt là trung điểm của CE,BF. Tam giác PQD là tam giác j? Chứng minh
Bài 8 cho tam giác ABC, phân giác AK. GIAO 3 đường phân giác của tam giác ABK cách đều 3 đỉnh của tam giác ABC.TÌNH số đo các góc trong tam giác ABC